【ケプラーの第3法則】衛星の公転周期を計算する方法

天文･宇宙

2021.10.22

天文宇宙検定2級で出題される「ケプラーの第3法則」と「公転周期の計算」の見方をまとめました。

【例題】人工衛星の公転周期
【例題】系外惑星系の親星の質量

【例題】人工衛星の公転周期

(問題)
ある人工衛星が以下のとおり公転しているとき、公転周期を計算せよ

・人工衛星は地球からの高度約1000kmの位置で周回している。
・地球の半径は約6000kmである。
・月は地球から約38万km離れている。
・月が地球を周回する公転周期は27日である。

(解答)
ケプラーの第3法則より、

(1) $\begin{eqnarray*} \frac{380000^3}{27^2}=\frac{(1000+6000)^3}{P^2}\\ P^2=\frac{7^3\times 10^9 \times 27^2}{38^3 \times 10^{12}}\\ P=0.065 \end{eqnarray*}$

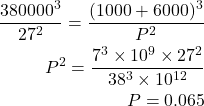
よって、約0.065日(94分)が人工衛星の公転周期と推定できる。

【例題】系外惑星系の親星の質量

(問)
地球質量の2倍の惑星が軌道長半径2天文単位、公転周期2年の軌道を公転している。
その場合、系外惑星系の親星(中心の恒星)の質量は太陽質量の何倍か。

(解答)
ケプラーの第三法則より2倍

【天文宇宙検定とは】対策･合格率･合格点まとめ【天文学の入門資格】

天文学の入門資格である天文宇宙検定2級とは?出題範囲、対策、合格率、合格点を中心にまとめをまとめました。