電験3種における電動機の所要出力とはずみ車効果(フライホイール効果)のポイント、例題トをまとめました。
【電動機応用】電動機の所要出力とはずみ車効果(フライホイール効果)
電動機が力F[N]、速度v[m/s]である物体を引っ張っているとき、電動機の所要出力P[W]は、次の式で表すことができます。
(1) ![]()
電動機がトルクT[N・m]、角速度 ω[rad/s]で回転しているとき、電動機の所要出力P[W]は、次の式で表すことができます。
(2) ![]()
上式のトルクTによってはずみ車は加速します。電動機が出力し続けて加速している間、この分のエネルギーがはずみ車に注入されます。電動機に直結するはずみ車の慣性モーメントをJ[kg・m2]として、加速が完了したときの電動機の角速度を![]() [rad/s]とすると、このはずみ車に蓄えられている運動エネルギー
[rad/s]とすると、このはずみ車に蓄えられている運動エネルギー![]() [J]は以下のとおりになります。
[J]は以下のとおりになります。
(3) ![]()
はずみ車効果(フライホイール効果)
はずみ車(フライホイール)とは、負荷のトルク変動が激しい場合、電動機と負荷の間に取り付ける鉄製の重い車です。
電動機で負荷とともに、はずみ車も併せて常時回転させておくことで、負荷トルクが急激に増加したとき、電動機の回転数は下がろうとしますが、はずみ車は慣性モーメントにより、等速運動を続けようとします。
そのため、負荷ははずみ車のエネルギー(トルク)をもらって回転し、電動機は定速運転ができます。
このように、負荷トルクの変動に応じてはずみ車がエネルギーを放出したり、吸収することをはずみ車効果(フライホイール効果)といいます。
はずみ車の重量がG[kg]、直径がD[m]のとき、はずみ車効果は![]() [kg⋅m2]となります。
[kg⋅m2]となります。
つまり、はずみ車の重量と直径が大きいほど効果は大きくなります。
慣性モーメントJの4倍である4J[kg⋅m2]をはずみ車効果といいます。
はずみ車効果が大きい場合、電動機の始動あるいは制動時間が短いときは軸に大きなねじれ応力がかかり軸を破損します。
また、慣性のため始動時間が長いときは電動機を加熱するので、電動機のスペックに合わせて適切なはずみ車を選定する必要があります。
【計算例】回転数が減少したときにはずみ車が放出するエネルギー
負荷の増加により、慣性モーメントJ=10[kg・m2]のはずみ車の回転数Nが1000[r/min]から500[r/min]に低下した。
このはずみ車が放出したエネルギーW[kJ]はいくらか。
【解答】
回転数Nのはずみ車の角速度ω[rad/s]は以下のとおり。
(4) ![]()
よって、回転数Nが1000のときの角速度を![]() 、500のときの角速度を
、500のときの角速度を![]() とすると、はずみ車の放出したエネルギーdWは以下のとおり。
とすると、はずみ車の放出したエネルギーdWは以下のとおり。
(5) 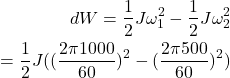
【計算例】回転数が減少したときにはずみ車が放出する平均エネルギー
慣性モーメントJ=10[kg・m2]のはずみ車が回転数Nが1000[min-1]で回転している。
①このはずみ車が持つ運動エネルギーW1kJ]はいくらか。
②このはずみ車に負荷が加わり、4秒間で回転数Nが1000[min-1]から 500[min-1]まで減速した間にはずみ車が放出する平均出力Wa[KW]の値はいくらか。
【解答①】
(6) ![]()
【解答②】
(7) 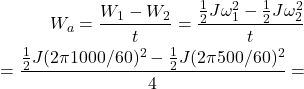
【例題】電動機に減速機を取り付けたときの負荷の回転速度、軸トルク、軸入力
電動機が減速機と組み合わされて負荷を駆動している。
電動機の回転速度![]() [min-1]、トルクTmが100[N・m]、減速機の減速比
[min-1]、トルクTmが100[N・m]、減速機の減速比![]() 、効率
、効率![]() であった。
であった。
このとき、①負荷の回転速度![]() [min-1]、②軸トルク
[min-1]、②軸トルク![]() [N・m]、③軸入力
[N・m]、③軸入力![]() [kW]はいくらになるか。
[kW]はいくらになるか。
【解答】
①負荷の回転速度
(8) ![]()
②負荷の軸トルク
(9) ![]()
③負荷の軸入力
(10) ![]()




コメント