【RL直列回路】時定数、電流、電圧、ラプラス変換

RL直列回路と時定数の関係についてまとめました。

【RL直列回路】時定数τ=L/R
【電流】計算式とグラフ
【抵抗電圧】計算式とグラフ
【コイル電圧】計算式とグラフ
【ラプラス変換】計算式の導出
【LTspice】RL回路の過渡応答シミュレーション

【RL直列回路】時定数τ=L/R

時定数 $\tau$ とは、緩和時間とも呼ばれ、回路の応答の速さを表す数値です。
時定数 $\tau$ と回路の応答の速さは「反比例」の関係にあります。
RL直列回路に流れる電流 $I$ 、抵抗にかかる電圧 $V_R$ 、コイルにかかる電圧 $V_L$ と時定数 $\tau$ の関係は次式で表せます。

(1) $\begin{eqnarray*} i(t)&=& \frac{V_i}{R} (1-V_i^{-\frac{R}{L}t})\\ V_R(t)&=& V_i (1-V_i^{-\frac{R}{L}t})\\ V_L(t)&=& V_i^{-\frac{R}{L}t}\\ \tau&=& \frac{L}{R} \end{eqnarray*}$

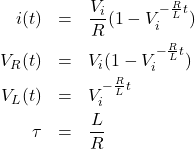
パラメータ	内容
$V_i$	入力電圧
$R$	抵抗値
$L$	コイルのインダクタンス
$V_R$	抵抗Rにかかる電圧
$V_L$	コイルLにかかる電圧
$\tau$	時定数（別名：緩和時間, 立ち上がり時間に比例）。定常状態の約63.2%まで到達する時間。

抵抗 $R$ が大きくなると立ち上がり・下がり時間（定常状態に達するまでの時間）は短くなります。
逆にコイルのインダクタンス $L$ が大きくなると立ち上がり・下がり時間（定常状態に達するまでの時間）は長くなります。

この関係は物理的に以下の意味をもちます.

抵抗が大きい･･･電流があまり流れず、コイルで電流に比例して発生する磁束も少しになるため, 電流変化も小さく定常状態にすぐに落ち着く(時定数は抵抗に反比例)
インダクタンスが大きい･･･コイルでインダクタンスに比例して磁束も多く発生するため, 電流変化も大きくなり定常状態に落ち着くのに時間がかかる(時定数はインダクタンスに比例)

一方, RC直列回路では, 時定数と抵抗は比例するので物理的な意味で理解するのも大事です.

【RC直列回路とは】時定数、電流、電圧、ラプラス変換

RC直列回路の原理と時定数、電流、電圧、ラプラス変換の計算方法についてまとめました。

【電流】計算式とグラフ

【RL直列回路】

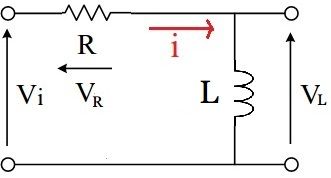
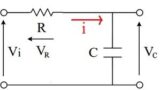
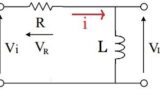
図のようなRL直列回路のコイルの電流式はつぎのようになります。

(2) $\begin{eqnarray*} i(t)&=& \frac{V_i}{R} (1-V_i^{-\frac{R}{L}t})\\ \tau&=&\frac{L}{R} \end{eqnarray*}$

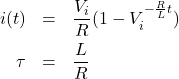
電流の式をグラフにすると以下のようになります。

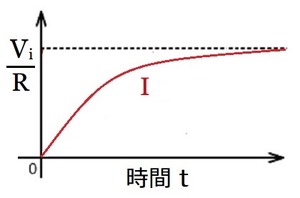
電流は時間 $t=0$ で $0$ となります。
そして、時間が経過して定常状態になると $\frac{V_i}{R}$ になります。
抵抗 $R$ が大きくなると立ち上がり時間（定常状態に達するまでの時間）は短くなります。
逆にコイルのインダクタンス $L$ が大きくなると立ち上がり時間（定常状態に達するまでの時間）は長くなります。

【RL直列回路】電流とグラフ

この記事では、RL直列回路の電流とグラフについてまとめました。

【抵抗電圧】計算式とグラフ

下図のようなRL直列回路の過渡応答の電圧式はつぎのようになります。

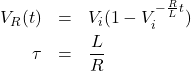
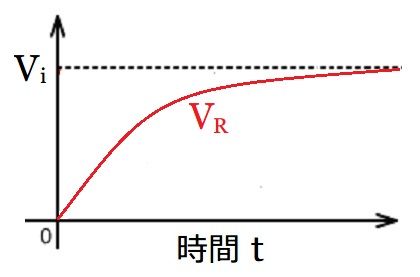
(3) $\begin{eqnarray*} V_R(t)&=&V_i (1-V_i^{-\frac{R}{L}t})\\ \tau&=&\frac{L}{R} \end{eqnarray*}$

電圧式をグラフにすると以下のようになります。

抵抗にかかる電圧は時間0で0となります。
そして、時間が経過して定常状態になると入力電圧と等価（ $V_R=V_i$ ）になります。
抵抗 $R$ が大きくなると立ち上がり時間（定常状態に達するまでの時間）は短くなります。
逆にコイルのインダクタンス $L$ が大きくなると立ち上がり時間（定常状態に達するまでの時間）は長くなります。

【RL直列回路】抵抗の電圧とグラフ

この記事では、RL直列回路の抵抗の電圧式とグラフを求める方法についてまとめました。

【コイル電圧】計算式とグラフ

下図のようなRL直列回路のコイルの電圧式はつぎのようになります。

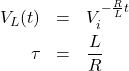
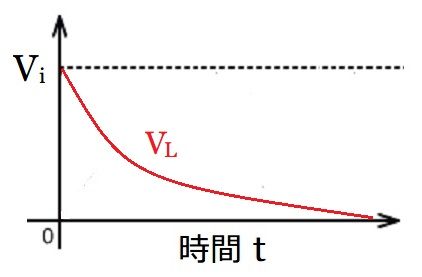
(4) $\begin{eqnarray*} V_L(t)&=&V_i^{-\frac{R}{L}t}\\ \tau&=&\frac{L}{R} \end{eqnarray*}$

電圧式をグラフにすると以下のようになります。

抵抗にかかる電圧は時間 $t=0$ で $V_i$ となります。
そして、時間が経過して定常状態になると0になります。
抵抗 $R$ が大きくなると立ち上がり時間（定常状態に達するまでの時間）は短くなります。
逆にコイルのインダクタンス $L$ が大きくなると立ち上がり時間（定常状態に達するまでの時間）は長くなります。

【RL直列回路】コイルの電圧とグラフ

この記事では、RL直列回路のコイルの電圧式とグラフを求める方法についてまとめました。

【ラプラス変換】計算式の導出

（ $V_i$ ：入力電圧、 $R$ ：抵抗値、 $L$ ：コイルのインダクタンス、 $V_R$ ：抵抗Rにかかる電圧、 $V_L$ ：コイルLにかかる電圧、 $i$ ：回路全体に流れる電流値）
RL直列回路の過渡応答の式をラプラス変換を用いて導出します。

ラプラス変換・逆ラプラス変換の対応表・公式

この記事では、ラプラス変換の対応表・公式について解説します。

キルヒホッフの定理より次式が成立します。

(5) $\begin{eqnarray*} V_i = L\frac{di(t)}{dt} + Ri(t) \end{eqnarray*}$

上式をラプラス変換すると

(6) $\begin{eqnarray*} \frac{V_i}{s} = sLI(s)+ RI(s)=\frac{I(s)}{Ls+R} \end{eqnarray*}$

となります。(V_iはステップ応答）
この式を電流 $I(S)$ について変形すると

(7) $\begin{eqnarray*} I(s)&=&\frac{V_i}{s(Ls+ R)}=\frac{\frac{V_i}{L}}{s(s+ \frac{R}{L})}=\frac{\frac{RV_i}{L}}{Rs(s+ \frac{R}{L})}\\ &=& \frac{V_i}{R} \left[ \frac{\frac{R}{L}}{s(s+\frac{R}{L})}\right]\\ &=& \frac{V_i}{R} \left[ \frac{\frac{R}{L}}{s(s+\frac{R}{L})}\right] \end{eqnarray*}$