【NumPy】連立方程式を解く numpy.linalg.solve

この記事では、Python言語とNumPyを用いて、連立方程式を解く方法をソースコード付きで解説します。

スポンサーリンク

連立方程式の解

PythonではNumPyを用いることで連立方程式を解くことが出来ます。

書式

X = numpy.linalg.solve(A, B)
パラメータ 説明
第1引数(A) 連立方程式AX=Bの正方行列A
第2引数(B) 連立方程式のベクトルB
戻り値(X) 連立方程式の解

PythonとNumPyのlinalg.solveを利用すると、連立方程式の解を求めることが出来ます。

ただし、連立方程式を行列の式(AX=B)に変換する必要があります。

例えば以下の連立の方程式の場合を考えます。

(1)   \begin{eqnarray*} \begin{cases} a_{11}x_1 + a_{12}x_2 = b_1 & \\ a_{21}x_1 + a_{22}x_2 = b_2 & \end{cases} \end{eqnarray*}

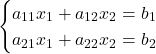
これを行列の式(AX=B)に変換すると次のようになります。

(2)   \begin{eqnarray*} AX=B \end{eqnarray*}

(3)   \begin{eqnarray*} A= \begin{bmatrix}a_{11} & a_{12} \a_{21} & a_{22} \end{bmatrix} , X= \begin{bmatrix}x_1\x_2 \end{bmatrix} , B= \begin{bmatrix}b_1\b_2 \end{bmatrix} \end{eqnarray*}

スポンサーリンク

ソースコード

サンプルプログラムのソースコードです。

# -*- coding: utf-8 -*-
import numpy as np


def main():

    A = np.array([[1.,3.]    # 行列Aの生成
                 ,[4.,2.]])
    B = np.array([1.,1.])   # 行列Bの生成

    X = np.linalg.solve(A, B)
    # 計算結果の表示
    print( "X=\n" + str(X) )


if __name__ == '__main__':
    main()
スポンサーリンク

実行結果

サンプルプログラムの実行結果は下記の通りです。

X=[ 0.1  0.3]

解Xが求まりました。(x1=0.1, x2=0.3)

おすすめ記事

Python入門 サンプル集
NumPy入門 サンプル集

コメント