Pythonモジュール「scikit-learn」で糖尿病患者のデータセットを読み込み、過学習を改善しながら回帰分析（重回帰、ラッソ回帰、リッジ回帰）する方法についてまとめました。
【はじめに】過学習とは
過学習とは、同じようなデータを使って学習し続けると、そのデータだけに強いモデルとなり、本番データに対する認識率が逆に下がってしまう減少です。
受験生で例えると、「ある特定の過去問ばかりを勉強した結果、過去問と傾向が異なる未知の問題が出てきたときに全く点がとれなくなる」ことです。
そのため学習する際は、評価データで精度向上度合いを確認し、ある程度飽和したところで学習を終了することが必要になります。
そのため、作成したモデルの精度は、学習に用いたデータではなく、未知のテストデータで測定してやる必要があります。
未知のデータに対する誤りを「汎化誤差」といい、汎化誤差が小さいことを「汎化能力が高い」といいます。
動画解説版
本記事の内容は動画でも解説しています。
【データセットの取得】糖尿病患者
まずは、load_diabetes()で糖尿病患者のデータセットを取得します。
# -*- coding: utf-8 -*-
from sklearn import datasets
# 糖尿病患者のデータセットをロード
dataset = datasets.load_diabetes()
print(dataset)
"""
{'data': array([[ 0.03807591, 0.05068012, 0.06169621, ..., -0.00259226,
0.01990842, -0.01764613],
....
'target': array([151., 75., 141., 206., 135., 97., 138., 63., 110., 310., 101.,
....
"""
データセットの中身は次のとおり。
| 種別 | 概要 |
|---|---|
| 説明変数 | sepal length（ガクの長さ）、sepal width（ガクの幅）、petal length（花弁の長さ）、petal width（花弁の幅）の4種類のデータ |
| 目的変数 | 糖尿病患者の1年後の進行状況(25～346) |
【データ特性の検証】散布図、ヒストグラム、ヒートマップ
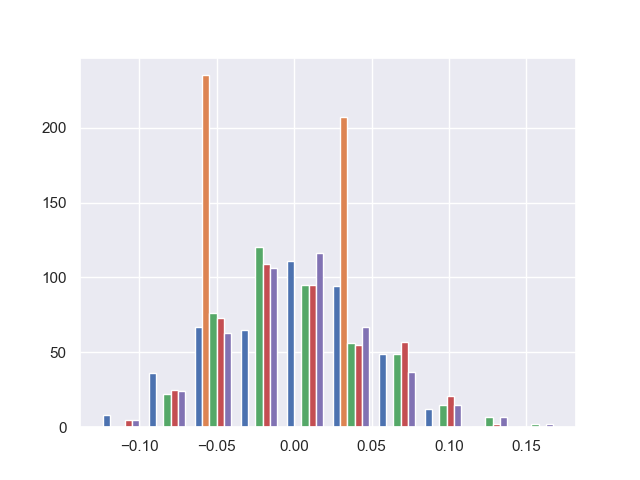
データセット（説明変数、目的変数）の特性を散布図、ヒストグラム、ヒートマップなどで観察してみます。
散布図
# -*- coding: utf-8 -*-
from sklearn import datasets
import matplotlib.pyplot as plt
import seaborn as sns
sns.set() # seabornのスタイルをセット
# 糖尿病患者のデータセットをロード
dataset = datasets.load_diabetes()
# 説明変数
X = dataset.data
# 目的変数
y = dataset.target
for i in range(X.shape[1]):
plt.plot(X[:, i], y, 'o')
plt.xlabel("X")
plt.ylabel("y")
plt.grid(True)
plt.show()
ヒストグラム
# -*- coding: utf-8 -*- from sklearn import datasets import matplotlib.pyplot as plt import seaborn as sns sns.set() # seabornのスタイルをセット # 糖尿病患者のデータセットをロード dataset = datasets.load_diabetes() # 説明変数 X = dataset.data # 目的変数 y = dataset.target plt.hist(X[:, 0:5]) plt.grid(True) plt.show()
相関ヒートマップ
# -*- coding: utf-8 -*- from sklearn import datasets import numpy as np import matplotlib.pyplot as plt import seaborn as sns import pandas as pd sns.set() # seabornのスタイルをセット # 糖尿病患者のデータセットをロード dataset = datasets.load_diabetes() # 説明変数 X = dataset.data # 目的変数 y = dataset.target # 相関係数を計算 corr = np.corrcoef(X.T, y) print(corr) # 相関係数をヒートマップ化 sns.heatmap(corr, annot=True) plt.show()
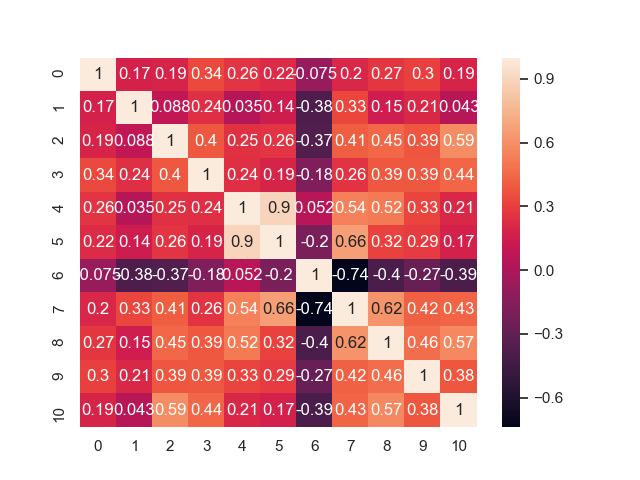
真ん中付近に「0.9」「-0.74」と説明変数同士でかなり高い相関値をもつものがあります。
この現象を「多重共線性」といいます。
多重共線性になると、変数間が独立ではないため解が計算できなかったり、信頼性が低下してしまいます。
そのため、高い相関値をもつ説明変数を取り除くなどの対策を取る必要があります。
【回帰】重回帰分析
まずは、何の工夫もせずにそのまま重回帰分析をしてみます。
# -*- coding: utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set() # seabornのスタイルをセット
# 糖尿病患者のデータセットをロード
dataset = datasets.load_diabetes()
# 説明変数
X = dataset.data
# 目的変数
y = dataset.target
# 学習用、テスト用にデータを分割（1:1）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
# 予測モデルを作成(重回帰)
clf = linear_model.LinearRegression()
# 学習
clf.fit(X_train, y_train)
# 回帰係数と切片の抽出
a = clf.coef_
b = clf.intercept_
# 回帰係数
print("回帰係数:", a)
print("切片:", b)
print("決定係数(学習用):", clf.score(X_train, y_train))
print("決定係数(テスト用):", clf.score(X_test, y_test))
"""
回帰係数: [ -20.41129305 -265.88594023 564.64844662 325.55650029 -692.23796104
395.62249978 23.52910434 116.37102129 843.98257585 12.71981044]
切片: 154.3589882135515
決定係数(学習用): 0.5730746555685652
決定係数(テスト用): 0.4377492256245158
"""
今回はホールド・アウト方でデータセットを訓練用とテスト用に２分割して精度検証しています。
| – | 関連記事 |
|---|---|
| 1 | ■【Python/scikit-learn】重回帰分析の使い方（過学習の改善・防止） |
結果（予測精度）は学習データで57%、テストデータでは43%となり過学習に陥っています。
過学習とは、訓練データにモデルが稼業適合（オーバーフィッティング）しすぎているため、学習データとテストデータの結果に差が大きく出て、精度が落ちてしまう現象です。
過学習を防ぐには、「訓練データの数を増やす」「正則化などで学習時に一定の制約を与える」「質の良い説明変数のみを使う」などの対策を施します。
訓練データを増やすという対策は実際には難しいので、正則化や説明変数の選択という手法をまず取ることが多いです。
【過学習防止法①】相関値の高い説明変数を除外
相関値の高い説明変数を除外してみましょう。
# -*- coding: utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set() # seabornのスタイルをセット
# 糖尿病患者のデータセットをロード
dataset = datasets.load_diabetes()
# 説明変数
X = dataset.data
# 相関の高い4番目～7番目の説明変数を除外
X = np.hstack((X[:, 0:5], X[:, 8:10]))
# 目的変数
y = dataset.target
# 学習用、テスト用にデータを分割（1:1）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=0)
# 予測モデルを作成(リッジ回帰)
clf = linear_model.Ridge()
# 学習
clf.fit(X_train, y_train)
# 回帰係数と切片の抽出
a = clf.coef_
b = clf.intercept_
# 回帰係数
print("回帰係数:", a)
print("切片:", b)
print("決定係数(学習用):", clf.score(X_train, y_train))
print("決定係数(テスト用):", clf.score(X_test, y_test))
"""
回帰係数: [ 56.45348132 -12.64593807 198.05710012 126.36651865 45.32494485
211.8317115 85.95664122]
切片: 151.37723470691103
決定係数(学習用): 0.36218623451960075
決定係数(テスト用): 0.30393630855490333
"""
学習データとテストデータの結果の差が小さくなり、過学習が改善されています。
| – | 詳細記事 |
|---|---|
| 1 | ■【scikit-learn】ラッソ回帰、リッジ回帰で過学習の改善・防止 |
【過学習防止法②】Lasso回帰（L1正則化）、リッジ回帰（L2正則化）
リッジ回帰は、直線回帰に正則化項（L2ノルム）を加えて、稼業適合（オーバーフィッティング）をしにくくした回帰分析です。
# -*- coding: utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set() # seabornのスタイルをセット
# 糖尿病患者のデータセットをロード
dataset = datasets.load_diabetes()
# 説明変数
X = dataset.data
# 目的変数
y = dataset.target
# 学習用、テスト用にデータを分割（1:1）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=0)
# 予測モデルを作成(リッジ回帰)
clf = linear_model.Ridge()
# 学習
clf.fit(X_train, y_train)
# 回帰係数と切片の抽出
a = clf.coef_
b = clf.intercept_
# 回帰係数
print("回帰係数:", a)
print("切片:", b)
print("決定係数(学習用):", clf.score(X_train, y_train))
print("決定係数(テスト用):", clf.score(X_test, y_test))
"""
回帰係数: [ -20.41129305 -265.88594023 564.64844662 325.55650029 -692.23796104
395.62249978 23.52910434 116.37102129 843.98257585 12.71981044]
切片: 154.3589882135515
決定係数(学習用): 0.3983270129832158
決定係数(テスト用): 0.3345645490979842
"""
学習データとテストデータの結果の差が小さくなり、過学習が改善されています。
# -*- coding: utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set() # seabornのスタイルをセット
# 糖尿病患者のデータセットをロード
dataset = datasets.load_diabetes()
# 説明変数
X = dataset.data
# 目的変数
y = dataset.target
# 学習用、テスト用にデータを分割（1:1）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=0)
# 予測モデルを作成(Lasso回帰)
clf = linear_model.Lasso()
# 学習
clf.fit(X_train, y_train)
# 回帰係数と切片の抽出
a = clf.coef_
b = clf.intercept_
# 回帰係数
print("回帰係数:", a)
print("切片:", b)
print("決定係数(学習用):", clf.score(X_train, y_train))
print("決定係数(テスト用):", clf.score(X_test, y_test))
"""
回帰係数: [ 0. -0. 397.28850539 0. 0.
0. -0. 0. 472.25346364 0. ]
切片: 151.99424541715777
決定係数(学習用): 0.4765923813915492
決定係数(テスト用): 0.3743169923017488
"""
過学習が少し改善されています。また、相関値の高い変数のうち一方が排除されやすいためモデル式も簡単になります。
| – | 詳細記事 |
|---|---|
| 1 | ■【scikit-learn】説明変数の選択・除外で過学習の改善・防止 |
【過学習防止法③】ヒストグラムから改善
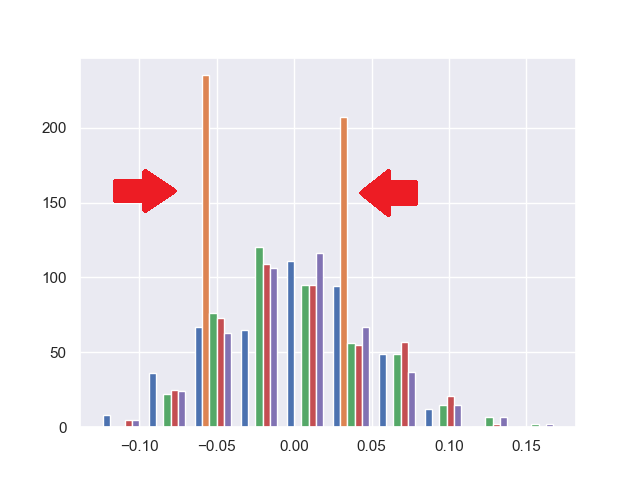
ヒストグラムを見てみると、オレンジ色の棒（2番目の説明変数）は、２つの値のみを取っています。
よって、2番目の説明変数が正か負のどちらの値になっているかでデータを分けて分析できそうです。
# -*- coding: utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set() # seabornのスタイルをセット
# 糖尿病患者のデータセットをロード
dataset = datasets.load_diabetes()
# 説明変数
X = dataset.data
# 2番目の説明変数が正の場合の値を抽出
new_X = X[X[:,1]>0]
new_X = np.hstack((new_X[:,0:1], new_X[:,2:10]))
# 目的変数
y = dataset.target
new_y = np.ones(new_X.shape[0])
j = 0
for i in range(X.shape[0]):
if X[i, 1] > 0:
new_y[j] = y[i]
j += 1
# 学習用、テスト用にデータを分割（1:1）
X_train, X_test, y_train, y_test = train_test_split(new_X, new_y, test_size=0.5, random_state=0)
# 予測モデルを作成(重回帰)
clf = linear_model.LinearRegression(normalize=True)
# 学習
clf.fit(X_train, y_train)
# 回帰係数と切片の抽出
a = clf.coef_
b = clf.intercept_
# 回帰係数
print("回帰係数:", a)
print("切片:", b)
print("決定係数(学習用):", clf.score(X_train, y_train))
print("決定係数(テスト用):", clf.score(X_test, y_test))
"""
回帰係数: [ 277.29294234 500.31554998 439.68983117 -475.51950795 173.84452198
-150.86666125 78.63507256 593.28585922 92.17250636]
切片: 136.50904152851012
決定係数(学習用): 0.584086429999823
決定係数(テスト用): 0.5808777752389886
"""
学習データとテストデータの結果の差がほとんどなくなり、過学習が大きく改善されています。
| – | 関連記事 |
|---|---|
| 1 | ■【Scikit-learn】機械学習入門・使い方 |
| 2 | ■【機械学習入門】アルゴリズム＆プログラミング |
| 3 | ■【Python入門】サンプル集 |
コメント