Pythonモジュール「scikit-learn」でL1正則化、L2正則化により過学習を改善しながらロジスティック回帰分析する方法についてまとめました。
【データセットの取得】アヤメの品種
まずは、load_iris()でアヤメの品種判別のデータセットを取得します。
# -*- coding: utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set() # seabornのスタイルをセット
# データセットをロード
dataset = datasets.load_iris()
X = dataset.data # 説明変数
y = dataset.target # 目的変数
y_name = dataset.target_names # 目的変数に対応する品種名
print("品種名：", y_name)
print("目的変数：", y)
print("説明変数：", X)
"""
品種名： ['setosa' 'versicolor' 'virginica']
目的変数： [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
説明変数： [[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
…
"""
データセットの中身は次のとおり。
| 種別 | 概要 |
|---|---|
| 説明変数 | 4つの値（がく片の長さ、がく片の幅、花弁の長さ、花弁の幅）。単位はいずれもcm。 |
| 目的変数 | アヤメの品種（3種類：setosa、versicolor、virginicaを0、1、2の数値ラベル化） |
【データ特性の検証】散布図、ヒストグラム、ヒートマップ
データセット（説明変数、目的変数）の特性を散布図、ヒストグラム、ヒートマップなどで観察してみます。
散布図
# -*- coding: utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set() # seabornのスタイルをセット
# データセットをロード
dataset = datasets.load_iris()
X = dataset.data # 説明変数
y = dataset.target # 目的変数
y_name = dataset.target_names # 目的変数に対応する品種名
# 各品種毎に散布図をプロット(各ラベルに50のデータがある)
for i in range(y_name.shape[0]):
# (がく片の長さ, がく片の幅)でプロット
plt.plot(X[i*50:i*50+50, 0], X[i*50:i*50+50, 1], 'o')
# (がく片の長さ, 花弁の長さ)でプロット
plt.plot(X[i*50:i*50+50, 0], X[i*50:i*50+50, 2], 'o')
# (がく片の長さ, 花弁の幅)でプロット
plt.plot(X[i*50:i*50+50, 0], X[i*50:i*50+50, 3], 'o')
plt.title(y_name[i])
plt.xlabel("X0")
plt.ylabel("x1, x2, x3")
plt.grid(True)
plt.show()
※各品種に対して、順に50セットのデータがデータセットに格納されています。
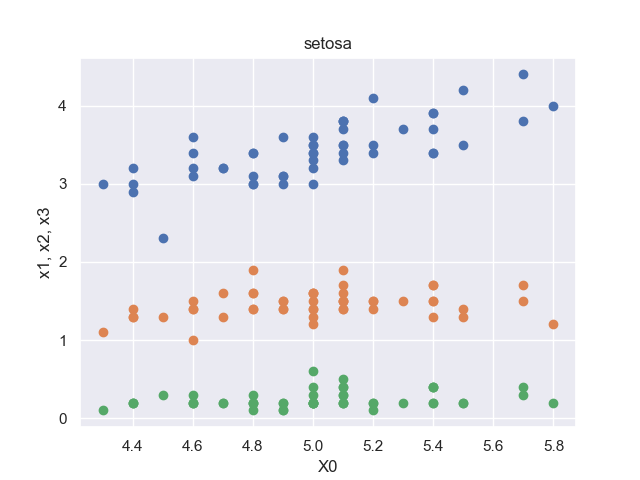
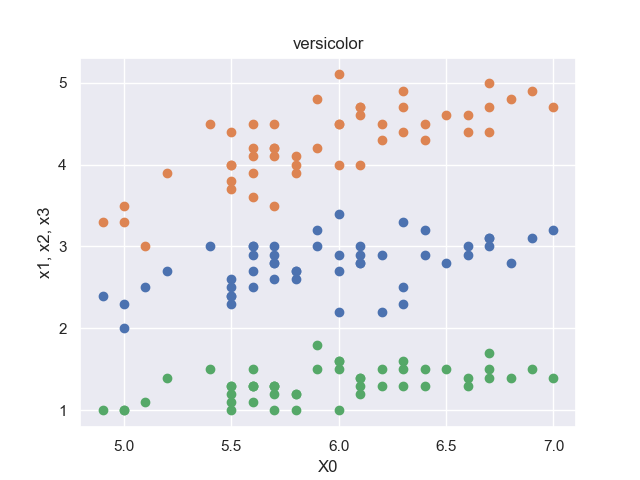
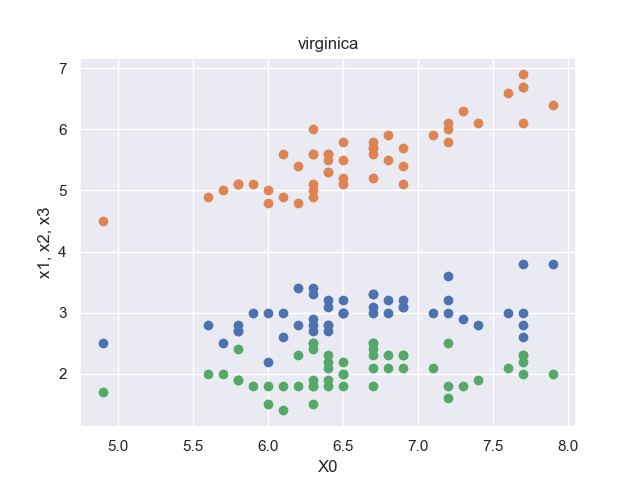
setosaの散布図のみ、オレンジの点群(がく片の長さ, 花弁の長さ)が真ん中に来ています。
よって、アヤメの品種が「setosa」か「setosa以外か」という判定は行いやすいだろうと推察できます。
ヒストグラム
# -*- coding: utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set() # seabornのスタイルをセット
# データセットをロード
dataset = datasets.load_iris()
X = dataset.data # 説明変数
y = dataset.target # 目的変数
y_name = dataset.target_names # 目的変数に対応する品種名
for i in range(y_name.shape[0]):
# (がく片の長さ, がく片の幅)でプロット
plt.hist(X[i*50:i*50+50, :])
plt.title(y_name[i])
plt.grid(True)
plt.show()
相関ヒートマップ
# -*- coding: utf-8 -*- from sklearn import datasets from sklearn.model_selection import train_test_split from sklearn import linear_model import numpy as np import matplotlib.pyplot as plt import seaborn as sns import pandas as pd sns.set() # seabornのスタイルをセット # データセットをロード dataset = datasets.load_iris() X = dataset.data # 説明変数 y = dataset.target # 目的変数 y_name = dataset.target_names # 目的変数に対応する品種名 # 説明変数同士の相関係数を計算 corr = np.corrcoef(X.T) print(corr) # 相関係数をヒートマップ化 sns.heatmap(corr, annot=True) plt.show()
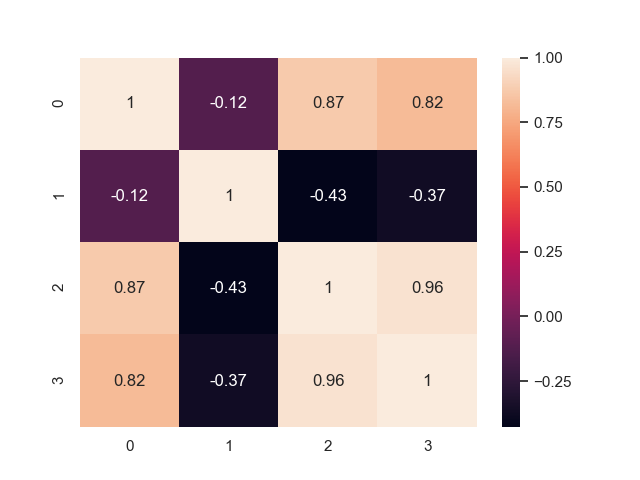
真ん中付近に「0.87」「0.82」「0.96」と説明変数同士でかなり高い相関値をもつものがあります。
この現象を「多重共線性」といいます。
多重共線性になると、変数間が独立ではないため解が計算できなかったり、信頼性が低下してしまいます。
そのため、高い相関値をもつ説明変数を取り除くなどの対策を取る必要があります。
【回帰】ロジスティック回帰分析
まずは、何の工夫もせずにそのままロジスティック回帰分析をしてみます。
# -*- coding: utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set() # seabornのスタイルをセット
# データセットをロード
dataset = datasets.load_iris()
X = dataset.data # 説明変数
y = dataset.target # 目的変数
y_name = dataset.target_names # 目的変数に対応する品種名
# 学習用、テスト用にデータを分割（1:1）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
# 学習（ロジスティック回帰）
clf = linear_model.LogisticRegression(random_state=0)
clf.fit(X_train, y_train)
# ロジスティック回帰の学習結果
a = clf.coef_
b = clf.intercept_
print("回帰係数:", a)
print("切片:", b)
# 予測精度の検証
print("スコア(訓練用データを入力):", clf.score(X_train, y_train))
print("スコア(テスト用を入力):", clf.score(X_test, y_test))
"""
回帰係数: [[ 0.37664729 1.25055622 -1.94787367 -0.8809699 ]
[ 0.49723257 -1.6214123 0.31913087 -0.87146961]
[-1.49621798 -0.59310092 1.90859707 1.70124234]]
切片: [ 0.23856784 0.7342459 -0.86078966]
スコア(訓練用データを入力): 0.92
スコア(テスト用を入力): 0.84
"""
今回はホールド・アウト方でデータセットを訓練用とテスト用に２分割して精度検証しています。
| – | 関連記事 |
|---|---|
| 1 | ■【Python/scikit-learn】重回帰分析の使い方（過学習の改善・防止） |
結果（予測精度）は学習データで92%、テストデータでは84%となり若干過学習に陥っています。
過学習とは、訓練データにモデルが稼業適合（オーバーフィッティング）しすぎているため、学習データとテストデータの結果に差が大きく出て、精度が落ちてしまう現象です。
過学習を防ぐには、「訓練データの数を増やす」「正則化などで学習時に一定の制約を与える」「質の良い説明変数のみを使う」などの対策を施します。
訓練データを増やすという対策は実際には難しいので、正則化や説明変数の選択という手法をまず取ることが多いです。
【過学習防止法】L1正則化、L2正則化
ヒートマップを見た時に説明変数同士で相関係数が高いものがありました。
しかしながら、今回のケースは説明変数の数が少ないため、相関の高いものを取り除くというのは現実的ではありません。
そのような場合は、ロジスティック回帰に正則化項（L2ノルム）を加えることで、稼業適合（オーバーフィッティング）を抑えることができます。
# -*- coding: utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set() # seabornのスタイルをセット
# データセットをロード
dataset = datasets.load_iris()
X = dataset.data # 説明変数
y = dataset.target # 目的変数
y_name = dataset.target_names # 目的変数に対応する品種名
# 学習用、テスト用にデータを分割（1:1）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
# 学習（ロジスティック回帰 + L1正則化）
clf = linear_model.LogisticRegression(random_state=0, penalty='l1', n_jobs=1, C=15)
clf.fit(X_train, y_train)
# ロジスティック回帰の学習結果
a = clf.coef_
b = clf.intercept_
print("回帰係数:", a)
print("切片:", b)
# 予測精度の検証
print("スコア(訓練用データを入力):", clf.score(X_train, y_train))
print("スコア(テスト用を入力):", clf.score(X_test, y_test))
"""
回帰係数: [[ 0.34476547 3.55978285 -4.68014219 0. ]
[-0.39624467 -3.89386144 1.34312456 -2.6994755 ]
[-3.5777949 -1.91844146 6.60045539 6.44262961]]
切片: [ 0. 10.9500214 -15.73786262]
スコア(訓練用データを入力): 0.9866666666666667
スコア(テスト用を入力): 0.96
"""
学習データとテストデータのスコアの差が小さくなり、過学習が改善されています。
# -*- coding: utf-8 -*-
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import linear_model
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set() # seabornのスタイルをセット
# データセットをロード
dataset = datasets.load_iris()
X = dataset.data # 説明変数
y = dataset.target # 目的変数
y_name = dataset.target_names # 目的変数に対応する品種名
# 学習用、テスト用にデータを分割（1:1）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
# 学習（ロジスティック回帰 + L2正則化）
clf = linear_model.LogisticRegression(random_state=0, penalty='l2', n_jobs=1, C=15)
clf.fit(X_train, y_train)
# ロジスティック回帰の学習結果
a = clf.coef_
b = clf.intercept_
print("回帰係数:", a)
print("切片:", b)
# 予測精度の検証
print("スコア(訓練用データを入力):", clf.score(X_train, y_train))
print("スコア(テスト用を入力):", clf.score(X_test, y_test))
"""
回帰係数: [[ 0.66524407 2.15628389 -3.42581672 -1.5952244 ]
[ 0.27279333 -3.08293152 0.91970137 -2.27832851]
[-3.39992172 -1.51071288 4.65769737 4.0098312 ]]
切片: [ 0.40883009 5.77538438 -3.89572019]
スコア(訓練用データを入力): 0.9866666666666667
スコア(テスト用を入力): 0.92
"""
過学習が少し改善されています。
【pickle】モデルの保存
# -*- coding: utf-8 -*- import pickle # モデルの保存 filepath = "test_model.dat" pickle.dump(clf, open(filepath, 'wb')) # モデルのロード load_clf = pickle.load(open(filename, 'wb'))
| – | 関連記事 |
|---|---|
| 1 | ■【Scikit-learn】機械学習入門・使い方 |
| 2 | ■【機械学習入門】アルゴリズム＆プログラミング |
| 3 | ■【Python入門】サンプル集 |
コメント