本ページでは、Python用制御工学モジュール「python-control」で2自由度機械システム(マス・ダンパ・バネ系)の伝達関数を求める方法とサンプルコードついて解説します。
状態方程式→伝達関数(2自由度機械システム)
2自由度機械システム(マス・ダンパ・バネ系)の状態方程式をpython-controlのss2tf()メソッドで伝達関数に変換します。
状態方程式
2自由度機械システムの状態方程式です。
(1) ![]()
(2) 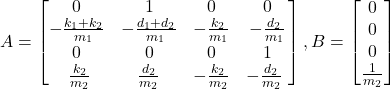
(3) ![]()
書式
sys = ss2tf(A, B, C, D)
A, B, C, Dは状態方程式の行列です。
戻り値sysは伝達関数です。
ソースコード
サンプルプログラムのソースコードです。
# -*- coding: utf-8 -*-
from control.matlab import *
from matplotlib import pyplot as plt
def main():
# マス・ダンパ・バネの係数
m1, m2 = 1.0, 1.2
d1, d2 = 0.1, 0.2
k1, k2 = 1.0, 1.5
# 状態方程式の行列
A = [[0., 1, 0, 0],
[-(k1+k2)/m1, -(d1+d2)/m1, -k2/m1 ,-d2/m1],
[0., 0., 0., 1.],
[-k2/m2, d2/m2, -k2/m2, -d2/m2] ]
B = [[0.],
[0.],
[0.],
[1./m2]]
C = [[0., 0., 1., 0.]]
D = [[0.]]
# 状態方程式から伝達関数を求める
sys_tf = ss2tf(A, B, C, D)
print(sys_tf)
if __name__ == "__main__":
main()
実行結果
サンプルプログラムの実行結果です。
0.8333 s^2 + 0.25 s + 2.083 ---------------------------------------------- s^4 + 0.4667 s^3 + 3.833 s^2 + 0.7917 s + 1.25



コメント