【Python/SciPy】スライディングモード制御のシミュレーション（極配置法）

この記事では、Python（SciPy+NumPy）を用いて、スライディングモード制御（極配置法）のシミュレーションを行う方法をソースコード付きで解説します。

## スライディングモード制御（極配置法）

Pythonの数値計算ライブラリ「NumPy」「SciPy」を用いることで行列計算や常微分方程式の計算を簡単に行うことが出来ます。
今回は、これらを用いて極配置法により設計した切換超平面をもつスライディングモード制御器のシミュレーションをやってみました。

①極配置法で切換超平面の設計（スライディングモード制御）

## ①切換超平面の設計

今回は以下のような1自由度振動系に対して切換超平面を設計します。

1自由度振動系の状態方程式はつぎのように表すことができます。
ただし $m=1, k=1, d=1$ とし、状態変数は $x1=x, x2=\dot{x}$ とします。

(1) $\begin{eqnarray*} \dot{x}=\begin{bmatrix} \dot{x_1} \\ \dot{x_2} \end{bmatrix} &=&Ax+Bu\\ &=&\begin{bmatrix} 0 & 1 \\ -\frac{k}{m} & -\frac{d}{m} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \end{bmatrix}u\\&=& \begin{bmatrix} 0 & 1 \\ -1 & -1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \end{bmatrix}u \end{eqnarray*}$

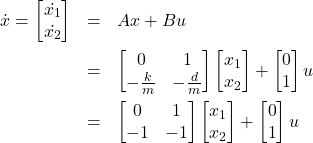
この状態方程式は既に正準系の形をしているので、座標変換は行いません。
（座標変換しても式は変化しません）
よって、 $A_{11}=0, A_{12}=1$ なので等価制御系は

(2) $\begin{eqnarray*} \dot{x}=(0-F)x\\ \end{eqnarray*}$

となります。
ここで、等価制御系の極の個数は1なので（1入力2次系より）、その極を負に配置するようなFを求めてやれば状態を原点に漸近させる切換超平面は求まります。
よって今回は $-5$ に極を配置することを考えれば、 $F=5$ となるので求めたい超平面は

(3) $\begin{eqnarray*} S=[5\hspace{10px}1] \end{eqnarray*}$

となります。

## ②コントローラの設計

次にコントローラ（制御入力）を設計します。
今回は「定常到達則」「比例到達則」「加速率到達則」を実装してみます。

定常到達則

定常到達則の場合、制御入力 $u$ は次のように求まります。

(4) $\begin{eqnarray*} u&=&-(SB)^{-1}(SAx+Qsgn(\sigma))\\ &=&-1(-x_1+4x_2+Qsgn(\sigma)) \end{eqnarray*}$

ここで、 $Q > 0$ となります。

比例到達則

定常到達則の場合、制御入力 $u$ は次のように求まります。

(5) $\begin{eqnarray*} u&=&-(SB)^{-1}(SAx+Qsgn(\sigma) + K\sigma)\\ &=&-1(-x_1+4x_2+Qsgn(\sigma) + K\sigma) \end{eqnarray*}$

ここで、 $Q > 0, K > 0$ となります。

加速率到達則

加速率到達則の場合、制御入力 $u$ は次のように求まります。

(6) $\begin{eqnarray*} u&=&-(SB)^{-1}(SAx+k_i|\sigma_i|^{\alpha}sgn(\sigma_i))\\ &=&-1(-x_1+4x_2+k_i|\sigma_i|^{\alpha}sgn(\sigma_i)) \end{eqnarray*}$

ここで、 $k_i > 0, 0 < \alpha < 1$ となります。

## ソースコード

サンプルプログラムのソースコードです。（Python3+SciPy+NumPy）

#-*- coding:utf-8 -*-
import matplotlib.pyplot as plt
import scipy.integrate as sp
import numpy as np
import random

# SMC制御系
def system(t, x):
    q = 5          # 定常項ゲインq
    k = 1          # 比例項のゲインk
    ka, a = 5, 0.8 # 加速率到達則のパラメータ
    s = [5.0, 1.0] # 切換超平面S

    # 戻り値用のリスト
    y = [0]*2

    # 切換関数の計算
    sigma = s[0]*x[0] + s[0]*x[1]

    # 制御入力u
    u = -(q * np.sign(sigma) - x[0] + 4*x[1]) # 定常到達則
    #u = -(q * np.sign(sigma) + k*sigma - x[0] + 4*x[1]) # 比例到達則
    #u = -(k * (np.abs(sigma)**a) * np.sign(sigma) - x[0] + 4*x[1]) # 加速率到達則

    # 外乱値を乱数で生成(値域は-1～1)
    d = random.uniform(-1, 1)

    # 常微分方程式（状態方程式）の計算
    dx1 = x[1]
    dx2 = -x[0] -x[1] + u + d

    # 計算結果を返す
    y[0] = dx1
    y[1] = dx2

    return y

def simulation(x0, end, step):
    x1 = []
    x2 = []
    t = []
    ode =  sp.ode(system)
    ode.set_integrator('dopri5', method='bdf', atol=1.e-2)
    ode.set_initial_value(x0, 0)
    t.append(0)
    x1.append(x0[0])
    x2.append(x0[1])

    while ode.successful() and ode.t < end - step:
        ode.integrate(ode.t + step)
        t.append(ode.t)
        x1.append(ode.y[0])
        x2.append(ode.y[1])

    return x1, x2, t

def draw_graph(x1, x2, t):
    plt.figure()
    # 左
    plt.subplot(121)
    plt.plot(t, x1, label='x_1')
    plt.plot(t, x2, label='x_2')
    plt.xlabel("Time")
    plt.ylabel("State variable")
    plt.legend()# 凡例表示
    plt.grid()  # グリッド表示

    # 右
    plt.subplot(122)
    plt.plot(x1, x2, label='x')
    plt.xlabel("x1")
    plt.ylabel("x2")
    plt.legend()# 凡例表示
    plt.grid()  # グリッド表示

    plt.show()


def main():
    # パラメータ
    x0 = [3.0, 1.0] # 初期値
    end = 10        # シミュレーション時間
    step = 0.01     # 時間の刻み幅

    # シミュレーション
    x1, x2, t = simulation(x0, end, step)

    # 結果をグラフ表示
    draw_graph(x1, x2, t)


if __name__ == "__main__":
    main()

## 実行結果

サンプルプログラムの実行結果です。
極配置法（極は-5）で設計した切換超平面Sとコントローラに定常到達則を用いています。

■参考文献
線形化フィードバックと組み合わせたスライディングモード制御

-	関連記事
①	■【Python】制御シミュレーション入門
②	■【制御工学入門】古典～現代制御の基本原理
③	■【Python入門】サンプル集
④	■【NumPy入門】サンプル集
⑤	■【SciPy入門】サンプル集