【部材断面】断面一次モーメント、断面二次モーメント、断面係数、断面二次半径の違いと計算式

構造力学における断面積、断面一次モーメント、図心、断面二次モーメント、断面係数、断面二次半径の違いと計算式と例題について紹介します。

【断面一次モーメント】断面の形状を数値化したもの
【断面二次モーメント】断面形状の曲げモーメントに対する硬さ(たわみの大きさ)
【断面係数Z】断面形状の曲げモーメントに対する強さ(許容曲げ応力度)
【断面二次半径】座屈に対する強さ
【補足】断面形状別の断面積A、断面二次モーメントI、断面係数Z

【断面一次モーメント】断面の形状を数値化したもの

断面一次モーメントとは、様々な部材の断面の形状を数値化するためのものです。
一般的には、断面の図心（重心）を求めるために必要な係数となります。

ある断面の全面積をA、断面内の微小な領域をdAとします。また、dAの座標を(x,y)をします。
このとき、x軸に関する断面一次モーメント $S_x$ 、y軸に関するx軸に関する断面一次モーメント $S_y$ はそれぞれ以下の式で計算できます。

(1) $\begin{eqnarray*} S_x=\int y dA \\ S_y=\int x dA \end{eqnarray*}$

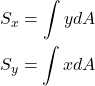
断面一次モーメントは、断面内の微小な領域dAに、そこまで距離(Sxの場合はx軸からの距離y)を乗じたものを断面領域全体で足し合わせ(積分)ています。
求めた断面一次モーメントSは、断面全体の面積Aで割ると断面の図心(xg, yg)を求めることができます。

(2) $\begin{eqnarray*} x_g=\frac{S_y}{A}\\ y_g=\frac{S_x}{A} \end{eqnarray*}$

【構造力学】断面一次モーメントとは?図心の計算方法

構造力学における断面一次モーメントとは?図心の計算方法について紹介します。

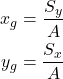
【断面二次モーメント】断面形状の曲げモーメントに対する硬さ(たわみの大きさ)

断面二次モーメントとは、「梁の曲げや変形に関わる係数」となります。
つまり、断面形状の曲げモーメントに対する「変形しにくさ=たわみの大きさ」を表します。
部材の曲げにくさは、材料の性質(鉄とかアルミとか木材とか)と形状（H型、I型、L型など）で決まり、断面二次モーメントは後者の指標となります。

ある部材の断面積について、x軸に関する断面二次モーメント $I_x$ 、y軸に関するx軸に関する断面二次モーメント $I_y$ はそれぞれ以下の式で計算できます。

(3) $\begin{eqnarray*} I_x=\int y^2dA \\ I_y=\int x^2dA \end{eqnarray*}$

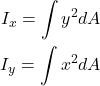
図心を求めるために計算していた断面一次モーメントの場合は基準座標系は気にしなくても良かったですが、断面二次モーメントはそれそのものを利用するため基準座標系が重要になります。
基準座標系によって、最終的に求められる断面の強度や剛性が異なりますので注意が必要です。

並行軸の定理

並行軸の定理とは、図心基準以外の任意の軸基準の断面二次モーメントを求めるためのものです。
図中点線の長方形断面をx方向にx、y方向にy移動させた時のx軸に関する断面二次モーメント $I'_x$ 、y軸に関するx軸に関する断面二次モーメント $I'_y$ はそれぞれ以下の式で計算できます。

(4) $\begin{eqnarray*} I'_x=I_x+A y^2 \\ I'_y=I_y+A x^2 \end{eqnarray*}$

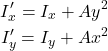
つまりは、図心基準の断面二次モーメントに移動距離の2乗と断面積Aを乗じたものを加算します。
H型、I型、L型などの複雑断面の断面二次モーメントを求めるのに重要な定理です。

【構造力学】断面二次モーメントとは?計算式と例題

構造力学における断面二次モーメントとは?計算式と例題について紹介します。

【断面係数Z】断面形状の曲げモーメントに対する強さ(許容曲げ応力度)

断面係数Zとは、梁部材の断面形状による曲げモーメントに対する強さ(どの程度の応力が加わっても永久変形しないか)を表します。
断面係数Zが大きくなるほど、曲げモーメントに対して強くなります。
断面二次モーメントと意味合いが似通っていますが、これは断面係数Zは以下のように断面二次モーメントIzから求めるためです。
中立軸z(断面の図心を通る軸)に対する断面二次モーメントがIz、中立軸zから外周までの距離がyのとき、断面係数Zは以下の式で計算できます。

(5) $\begin{eqnarray*} Z=\frac{I_z}{y} \end{eqnarray*}$

断面係数Zは、梁の曲げ応力度σを計算する際に使用します。
梁に加わる曲げモーメントがMのとき、曲げ応力度σは以下のようになります。

(6) $\begin{eqnarray*} \sigma=\frac{M}{Z} \end{eqnarray*}$

部材の種類によって、許容(曲げ)応力度は決まるため、「曲げ応力度σ　＜　許容(曲げ)応力度」となるように設計を行います(許容応力度設計)。

曲げモーメントMと曲げ応力度σは比例関係にあります。
一方、断面係数Zと曲げ応力度σは反比例関係にあるます。

よって一般的に

・曲げモーメントMは小さい方が良い
・断面係数Zは大きい方が良い

といえます。

断面係数と断面二次モーメント

断面係数Zは部材の断面形状が曲げに対する強さ(どの程度の曲げ応力度が加わっても永久変形しないか)を表します。
一方、断面二次モーメントは部材の断面形状が曲げに対する硬さ(変形が小さい=たわみが小さい)かを表します。
そのため、断面係数Zは「許容応力度」の計算、断面二次モーメントは「たわみの計算」に用いられます。

【構造力学】断面係数とは?断面二次モーメントとの違いと計算式と例題

構造力学における断面係数Zとは?計算式と例題について紹介します。

【断面二次半径】座屈に対する強さ

断面二次半径i[mm]は、梁部材が圧縮力を受けたときの座屈に対する強さを計算をするときに用いられます。
全断面の二次モーメント $i_z^2A$ が断面二次モーメントIzと等しくなるとき、この中立軸z(図心を通る軸)からの距離izを断面二次半径といいます。

(7) $\begin{eqnarray*} I_z=i_z^2A \\ i_z=\sqrt{\frac{I_z}{A}} \end{eqnarray*}$

【構造力学】断面二次半径、細長比と座屈長さとは?計算式と例題

構造力学における断面二次半径とは?計算式と例題について紹介します。

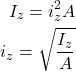
【補足】断面形状別の断面積A、断面二次モーメントI、断面係数Z

断面形状	断面積A	断面二次モーメントI	断面係数Z
①長方形	$bh$	$\frac{bh^3}{12}$	$\frac{bh^2}{6}$
②中空長方形	$bh-b_1h_1$	$\frac{bh^3-b_1h_1^3}{12}$	$\frac{bh^3-b_1h_1^3}{6h}$
③円形	ー	$\frac{\pi d^4}{64}$	$\frac{\pi d^3}{32}$
④中空円形	ー	$\frac{\pi(d^4-d_1^4)}{64}$	$\frac{\pi(d^3-d_1^3)}{32d}$
⑤楕円形	ー	$\frac{\pi ab^3}{4}$	$\frac{\pi ab^2}{4}$
⑥三角形	ー	$\frac{bh^3}{36}$	$Z_1=\frac{bh^2}{12}, Z_2=\frac{bh^2}{24}$
⑦台形	ー	ー	ー
⑧T形	ー	ー	ー
⑨I形	ー	$\frac{bd^3-h^3(b-t)}{12}$	$\frac{bd^3-h^3(b-t)}{6d}$
⑩L形	ー	ー	ー
⑪U形	ー	ー	ー
⑫コの字	ー	ー	ー
⑬H形	ー	ー	ー
⑭リップ溝形	ー	ー	ー