構造力学における断面二次半径とは?計算式と例題について紹介します。
【断面二次半径とは】座屈に対する強さ
断面二次半径i[mm]は、座屈の計算をするときに用いられる定数です。
全断面の二次モーメント![]() が断面二次モーメントIzと等しくなるとき、この中立軸z(図心を通る軸)からの距離izを断面二次半径といいます。
が断面二次モーメントIzと等しくなるとき、この中立軸z(図心を通る軸)からの距離izを断面二次半径といいます。
(1) 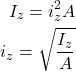
【座屈長さ】支持条件に対する座屈部分の長さ
座屈長さLbとは、支持条件に対する座屈部分の長さのことです。
座屈長さ係数A(支持条件(境界条件)により決まる)のとき以下の式で計算できます。
(2) ![]()
【細長比とは】限界細長比
細長比λは、座屈長さLb、断面二次半径izのとき以下の式で計算できます。
(3) ![]()
細長比が小さければ小さいほど座屈耐力は大きくなり、逆の場合は座屈耐力が小さくなります。
例えば、ある柱に小さい圧縮応力が作用しているとき、柱はできるだけ細くしたいとします。このとき、建築基準法で細長比に制限があるため、細くするには限界があります。
柱の細長比 λ=200以下
梁の細長比 λ=250以下
柱のほうが細長比がより厳しい制限なのは、梁と違って、柱は常に圧縮力を負担しているためです。
細長比を用いて座屈耐力を計算すると、細長比が小さいほど座屈耐力は大きくなり、降伏強度を越えてしまう矛盾が発生するため、弾性領域までしか検討できません。(本来、座屈耐力が降伏強度に達すると、部材は降伏するため座屈耐力は減少する)。
そのため、非弾性領域の座屈耐力を計算する場合は、「限界細長比」を用います。

【部材断面】断面一次モーメント、断面二次モーメント、断面係数、断面二次半径の違いと計算式
構造力学における断面積、断面一次モーメント、図心、断面二次モーメント、断面係数、断面二次半径の違いと計算式と例題について紹介します。

構造力学・構造計算入門
構造力学の基礎、計算式、例題集について入門者向けにまとめました。

コメント