単純支持梁、斜め梁(はり)における支点反力の計算方法について紹介します。
集中荷重が加わったときの支点反力、曲げモーメント、せん断力
● 支点反力とは梁が支点で支えられているときに支点に作用する反力(RA、RB)です。
支点反力を求めるには、力とモーメントの釣り合いを使います。
① 鉛直方向の力の釣り合い式は以下のとおりです。
(1) ![]()
② A点をモーメントの基準点としたとき、モーメント(基準点からの距離×作用する力)の釣り合い式は以下のとおりです。
(モーメントの釣り合いの式から支点反力RBが求まります)
(2) 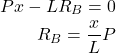
③ (1)(2)式より支点反力RAは以下のようになります。
(3) ![]()
●曲げモーメントとせん断力は、集中荷重の作用点の左側(0≦x<L1)と右側(L1<x≦L)で仮想切断して求めます。
(仮想切断は、実際に切断するわけではないため、切断面には断面力(内力)が生じます)
①集中荷重より左側(0≦x<L1)で仮想切断したとき、力の釣り合いよりせん断力は以下のようになります。
(4) 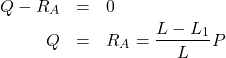
点Xを回転中心(時計回りを正)としてモーメントの釣り合いを考えるとMは以下のように求まります。
(回転中心を点X=切断点にしない場合、未知数であるせん断力も釣り合い式に入るため解けません)
(5) 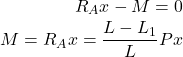
②集中荷重より右側(L1<x≦L)で仮想切断したとき、せん断力は以下のようになる。
(6) 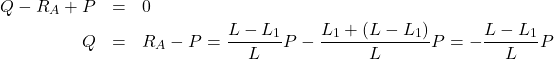
点Xを回転中心(時計回りを正)としてモーメントの釣り合いを考えるとMは以下のように求まります。
(7) 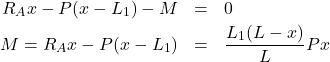
仮に、集中荷重は梁の中央に与えられていた場合、![]() より
より
(8) ![]()
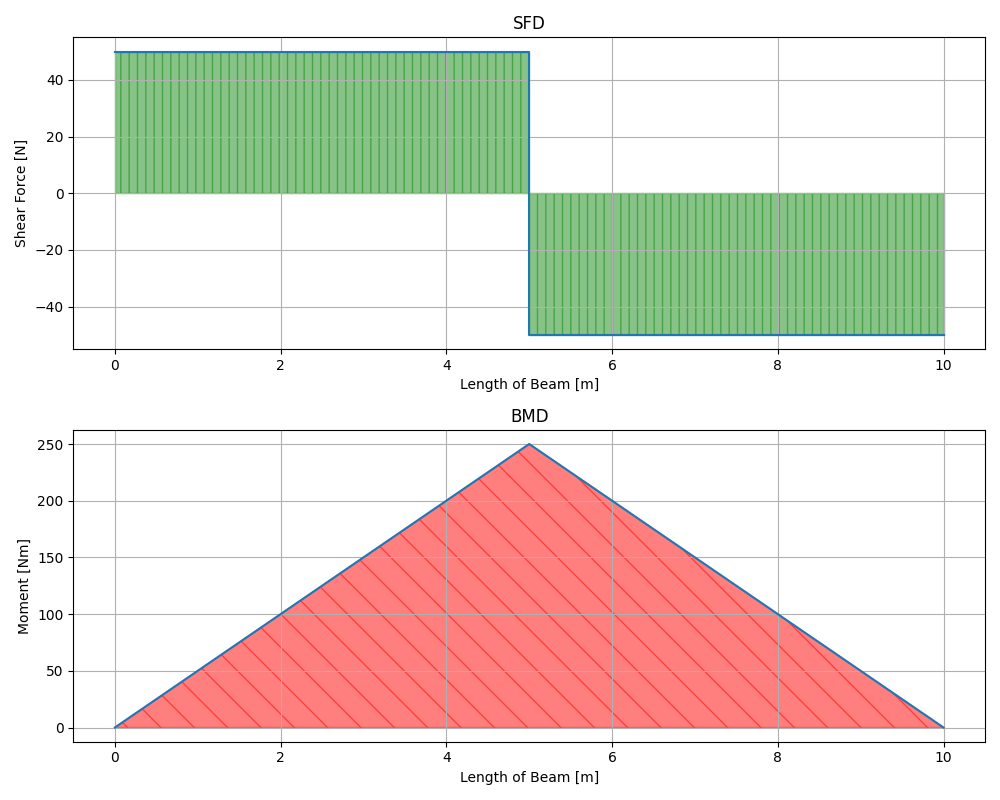
例
P=100[N]、L=10[m]、L1=5[m]のときのSFD(せん断力図)とBMD(曲げモーメント図)は以下のようになります。
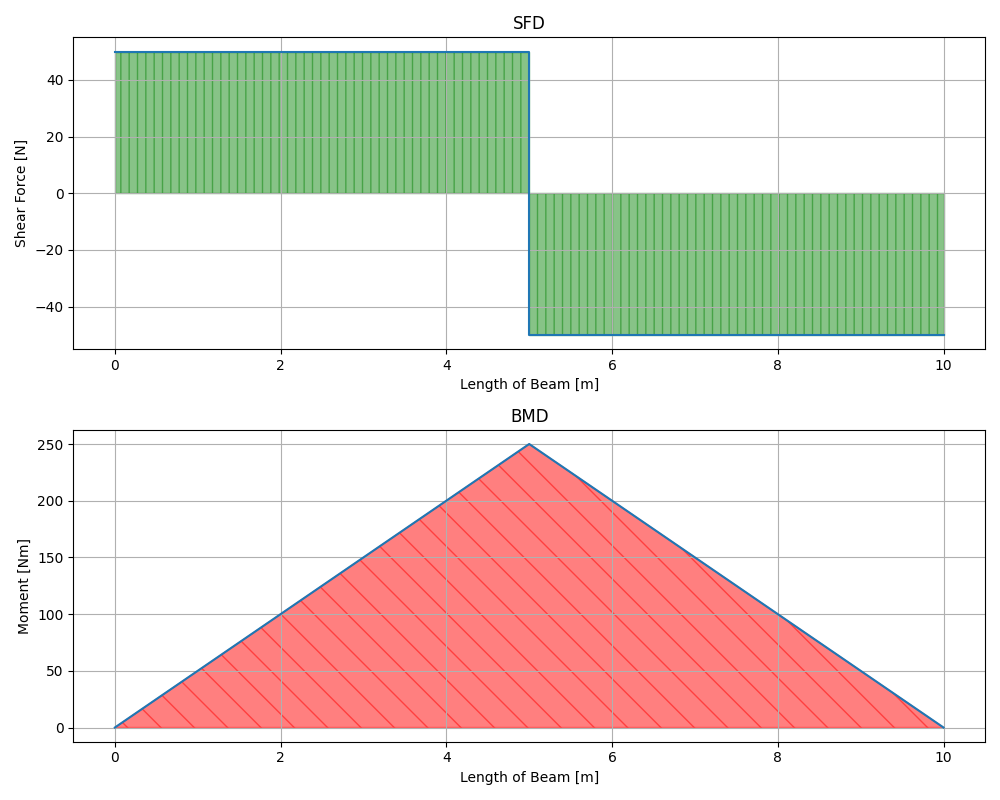
※モーメントの最大値は「PL/4=100*10/4=250[N]」となります。
単純梁に分布荷重が加わったときの支点反力(両端ピン、片側ピン)
分布荷重wが単純梁に一様に加わっている場合、中央に集中荷重wLが加わっているものと置き換えて考えます。
あとは、力のつり合いとモーメントの釣り合いを使います。
●力の釣り合い
(9) ![]()
●モーメントのつり合い
モーメントの定義は「基準点からの距離×作用する力」です
A点をモーメントの基準点とします。するとモーメントの釣り合いの式から支点反力RBが求まります。
(10) 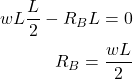
(1)(2)式より支点反力RAは以下のようになります。
(11) ![]()

コメント