【制御理論】同値変換の不変性

この記事では、同値変換の不変性(状態方程式を同値変換してもシステムの性質は変わらない)について紹介します。

同値変換の不変性証明
関連ページ

同値変換の不変性証明

状態方程式を正則変換（同値変換）してもシステムの性質は変わらないことを示してみたいと思います。

同値変換した状態方程式と出力方程式は次式で与えられます。

(1) $\begin{eqnarray*} \dot{\xi}(t)=\tilde{A}\xi (t)+T\tilde{B}u(t)\\ y(t)=\tilde{C}T^{-1}\xi (t)+Du(t) \end{eqnarray*}$

ここで同値変換した状態方程式を伝達関数に変換すると次のようになります。

(2) $\begin{eqnarray*} \tilde{G}(s)&=&D+\tilde{C}(SI-\tilde{A})^{-1}\tilde{B}\\ &=&D+CT^{-1}(sI-TAT^{-1})^{-1}TB\\ &=&D+C(sI-A)^{-1}B\\ &=&G(s) \end{eqnarray*}$

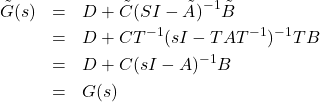
上式より状態方程式を同値変換しても伝達関数行列は変わらないことがわかります。よってシステムの性質（固有値など）は不変となります。

（入力uと出力yは同値変換しても変わらないので、入出力関係を表す伝達関数の値は変化しない）

この結果は、状態変数 $x$ はどういう風に取っても良いことを示します。

関連ページ

【システム制御理論入門】古典～現代制御の原理を解説

制御工学（古典～現代制御）の基本的なアルゴリズムや公式について入門者向けに解説します。

【Python】制御工学シミュレーション入門

プログラミング言語「Python」を用いて、無料で簡単に制御工学シミュレーションを行う方法を紹介します。