【オプティカルフローとは】推定の原理・特徴・計算式

オプティカルフローとは？移動量の推定方法、原理、計算式についてまとめました。

オプティカルフローとは
【仮定】オプティカルフローの拘束方程式
【推定問題】Aperture problem
関連ページ

オプティカルフローとは

オプティカルフローとは、デジタル画像中の物体の動きを「ベクトル」で表したものです。
主に移動物体の検出や、その動作の解析などによく用いられています。
しかしオプティカルフロー(=物体の移動ベクトル)を一意的に求めることは困難です。
一般的には推定によって動き（ベクトル）を求めます。
オプティカルフローを推定する手法は代表的なモノに「LucasKanade法」や「Horn-Schunk法」があります。
この記事では、まずオプティカルフローの基本的な考え方について紹介します。

【仮定】オプティカルフローの拘束方程式

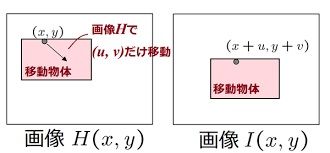
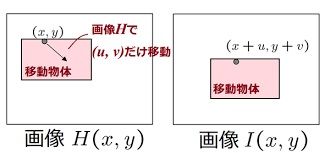
上図のような連続する2枚の画像 $H, I$ を撮影したとします。
このとき、画像中にある移動物体の動きを調べたいとすると、画像 $H$ 上の移動物体の画素が、画像I上でどこまで移動したかを求める必要があります。
ここで, 画像 $H, I$ に対して以下の仮定を置きます。

仮定

①画素が移動しても画素値は不変
②画像は滑らか(微分可能)
③画素の移動量は小さい(1画素以下)

画像 $I$ における座標 $(x+u,y+v)$ の画素値を $I(x+u,y+v)$ 、画像 $H$ における座標 $(x,y)$ の画素値を $H(x,y)$ とします。
このとき、仮定①より「画素が移動しても画素値は変わらない」ことから以下の等式が成立します。

(1) $\begin{eqnarray*} I(x+u,y+v)=H(x,y) \end{eqnarray*}$

仮定②③より $I(x+u,y+v)$ を一次項までテイラー展開すると以下の式が得られます。

(2) $\begin{eqnarray*} I(x+u,y+v)\approx I(x,y)+\frac{\partial I}{\partial x}u+\frac{\partial I}{\partial y}v \end{eqnarray*}$

(2)式を(1)式に代入すると以下の式が得られます。

拘束方程式

(3) $\begin{eqnarray*} \frac{\partial I}{\partial x}u+\frac{\partial I}{\partial y}v&=&-(I(x,y)-H(x,y))\\ \frac{\partial I}{\partial x}u+\frac{\partial I}{\partial y}v&=&-\Delta I\\ I_xu+I_yv&=&-\Delta I \end{eqnarray*}$

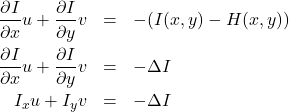
(3)式は「オプティカルフローの拘束方程式」と呼ばれる重要な式です。
仮定①が成り立つ、画像中のすべての画素がこの拘束式を満たします。

【推定問題】Aperture problem

オプティカルフローの拘束方程式は以下のように表せます。

(4) $\begin{eqnarray*} \nabla I・[u\hspace{7pt}v]^T=&-\Delta I \end{eqnarray*}$

(4)式は|エッジの勾配|と|エッジに対する移動ベクトルの垂直運動成分|の内積が画像の差分に等しいことを表しています。
この数式の意味を整理すると以下のようになります。

①エッジの勾配方向の移動ベクトルは求めることができる
②エッジと平行な移動ベクトルは求めることができない

これを窓問題（Aperture problem）といいます。

オプティカルフローの拘束方程式は1画素辺り1つだけ得られます。
しかし、拘束方程式1つには未知数が2つ(画素の移動ベクトル $u, v$ )あります。
よって、最初に述べたとおり、連立方程式を解いてもuとvの解が複数になるため、一意に求めることが出来ません。
なので、複数出てくる解の候補達から最も正解に近い解 $(u,v)$ を推定してやる必要があります。
これがオプティカルフローの推定問題です。
推定方法については古くからたくさん研究されており、その中でも有名なのが「LucasKanade法」や「Horn-Schunk法」です。
「LucasKanade法」については以下ページで解説しています。