画像処理における大津の手法(判別分析法)を用いた二値化処理の原理や計算式についてまとめました。
大津の二値化処理(判別分析法)と原理
本ページの内容は以下動画で解説しています。
大津の手法(判別分析法)は、自動的に閾値を決定して二値化処理を行う手法の1つです。
この手法では、分離度が最も大きくなるときの閾値を求めます。
閾値を求めるまでの処理手順は次の通りです。
① 入力画像![]() (1チャンネル)のヒストグラムを求めます。
(1チャンネル)のヒストグラムを求めます。

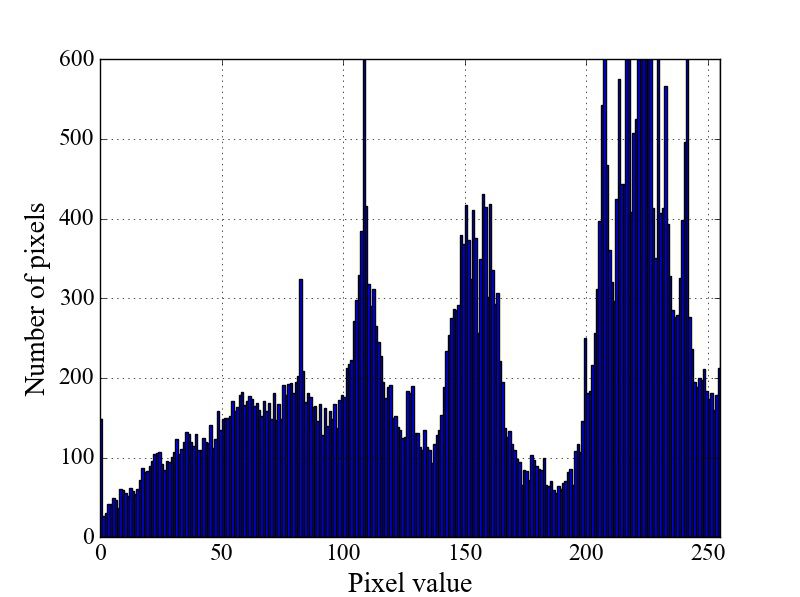
②ヒストグラムから、画素値の最大値![]() 、最小値
、最小値![]() 、平均値
、平均値![]() を求めます。
を求めます。
③ ![]() ~
~![]() の範囲内で、ある閾値
の範囲内で、ある閾値![]() を選びます。
を選びます。
④ 閾値![]() でヒストグラムを2つのクラス(Class)に分けます。
でヒストグラムを2つのクラス(Class)に分けます。
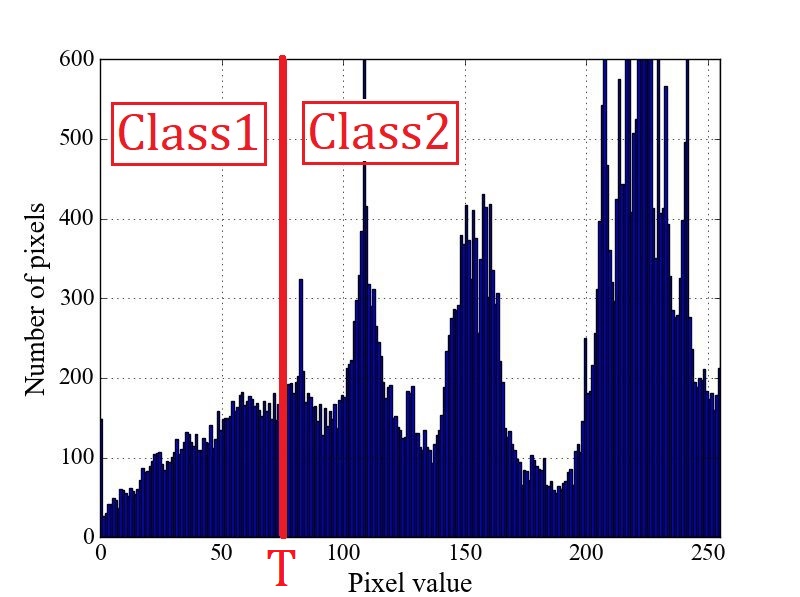
⑤ クラス1の分散![]() 、平均値
、平均値![]() 、画素数
、画素数![]() を求めます。
を求めます。
⑥ クラス2の分散![]() 、平均値
、平均値![]() 、画素数
、画素数![]() を求めます。
を求めます。
⑦ 以下の式からクラス内分散![]() とクラス間分散
とクラス間分散![]() を求めます。
を求めます。
(1) 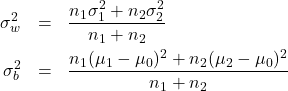
⑧ 手順⑦で求めた2つの分散から、分離度![]() (クラス内分散とクラス間分散の比)を求めます。
(クラス内分散とクラス間分散の比)を求めます。
(2) ![]()
⑨ 手順③~⑧を繰り返し、分離度![]() を
を![]() ~
~![]() の範囲内にある全ての
の範囲内にある全ての![]() の分だけ求めます。
の分だけ求めます。
⑩ 分離度![]() が最大になるときの
が最大になるときの![]() を二値化処理に用いる閾値に決定します。
を二値化処理に用いる閾値に決定します。
【実装例】プログラミング
プログラミング言語による実装例を以下にまとめました。
https://algorithm.joho.info/programming/python/opencv-otsu-thresholding-py/

【画像処理超入門】アルゴリズムの仕組みと実装方法を簡単に解説
画像処理超アルゴリズムの仕組みとプログラミングによる実装方法を簡単に解説します。


コメント