画像処理における空間フィルタリングと畳み込み演算の計算方法についてまとめました。
空間フィルタリングとは
本ページの内容は以下動画で解説しています。
空間フィルタリング (Spatial filtering) とは、入力画像の注目する画素値だけでなく、その近傍(周囲)にある画素値も利用し、出力画像の画素値を計算する処理です。
この計算のことを畳み込み演算、もしくはマスク演算といいます。
空間フィルタリングを利用することで、例えば、以下のように画像から輪郭だけを取り出すことができます。
■入力画像(左)と出力画像(右)


畳み込み演算の計算方法
空間フィルタリングでは、畳み込み演算により出力画像を求めます。
例えば、入力画像![]() とカーネル
とカーネル![]() が次のように与えられたします。
が次のように与えられたします。
(1) ![Rendered by QuickLaTeX.com \begin{eqnarray*} I= \left[ \begin{array}{ccccc} I(0, 0) & I(1, 0) & I(2, 0) & I(3, 0)\\ I(0, 1) & I(1, 1) & I(2, 1) & I(3, 1)\\ I(0, 2) & I(1, 2) & I(2, 2) & I(3, 2)\\ I(0, 3) & I(1, 3) & I(2, 3) & I(3, 3)\\ \end{array} \right], K= \left[ \begin{array}{ccccc} K(0, 0) & K(1, 0) & K(2, 0)\\ K(0, 1) & K(1, 1) & K(2, 1)\\ K(0, 2) & K(1, 2) & K(2, 2)\\ \end{array} \right] \end{eqnarray*}](https://algorithm.joho.info/wp-content/ql-cache/quicklatex.com-f817b1890a38ddf6c5a70846bd8ec885_l3.png)
このとき、出力画像![]() の端以外の画素値は次のように計算します。
の端以外の画素値は次のように計算します。
(2) ![Rendered by QuickLaTeX.com \begin{eqnarray*} I'= \left[ \begin{array}{ccccc} I'(0, 0) & I'(1, 0) & I'(2, 0) & I'(3, 0)\\ I'(0, 1) & I'(1, 1) & I'(2, 1) & I'(3, 1)\\ I'(0, 2) & I'(1, 2) & I'(2, 2) & I'(3, 2)\\ I'(0, 3) & I'(1, 3) & I'(2, 3) & I'(3, 3)\\ \end{array} \right] \end{eqnarray*}](https://algorithm.joho.info/wp-content/ql-cache/quicklatex.com-befe98a9773508a42db11f61e7f7d70d_l3.png)
■注目画素![]() について
について
(3) 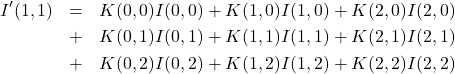
■注目画素![]() について
について
(4) 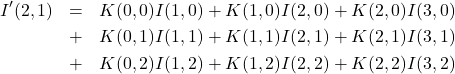
■注目画素![]() について
について
(5) 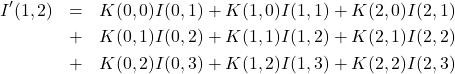
■注目画素![]() について
について
(6) 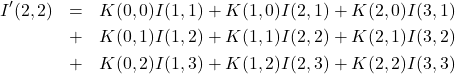
- カーネル
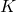 のサイズ
のサイズ
- 近傍の画素数(
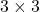 なら8近傍)
なら8近傍)
- 近傍の画素数(
- カーネル
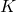 の要素
の要素
- 近傍にある画素の重み(目的や用途に応じて変える)
端の画素の処理

入力画像の端の画素を注目画素とした時は、近傍の画素数が不足します。
例えば、![]() に隣接する画素は
に隣接する画素は![]() ,
, ![]() ,
, ![]() の3つしかありません。
の3つしかありません。
その場合の処理方法は特に定義されていないため、自分で定義します。
色々なやり方が考えられますが、簡単化のため今回は次のように処理します。
- 輪郭抽出に使う場合
- 出力画像の端の画素値は全て0にする
- 平滑化処理に使う場合
- 出入力画像の画素値をそのまま出力画像の画素値にする
畳み込み演算の計算式
カーネルサイズが![]() の場合、畳み込み演算の計算を定式化すると次のようになります。
の場合、畳み込み演算の計算を定式化すると次のようになります。
(7) 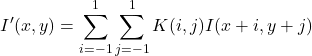
畳み込み演算の計算例
入力画像![]() とカーネル
とカーネル![]() が次のように与えられたとき、出力画像
が次のように与えられたとき、出力画像![]() を求めよ。
を求めよ。
(8) ![Rendered by QuickLaTeX.com \begin{eqnarray*} I= \left[ \begin{array}{ccccc} 11& 12 & 13 & 14\\ 21& 22 & 23 & 24\\ 31& 32 & 33 & 34\\ 41& 42 & 43 & 44\\ \end{array} \right], K= \left[ \begin{array}{ccccc} -1 & -2 & -1\\ 0 & 0 & 0\\ 1 & 2 & 1\\ \end{array} \right] \end{eqnarray*}](https://algorithm.joho.info/wp-content/ql-cache/quicklatex.com-413058e79090e3e531c8b0b61560ea5f_l3.png)
解説
入力画像![]() とカーネル
とカーネル![]() を畳み込み演算してやると
を畳み込み演算してやると
(9) 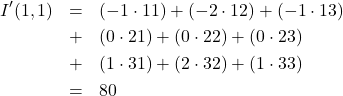
(10) 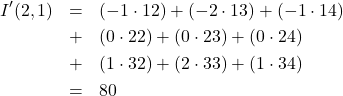
(11) 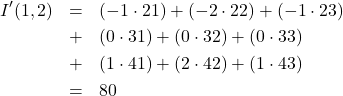
(12) 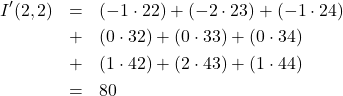
となります。今回、端の画素値は全て0にすることにします。
(13) ![]()
すると、出力画像![]() は次のようになります。
は次のようになります。
(14) ![Rendered by QuickLaTeX.com \begin{eqnarray*} I'= \left[ \begin{array}{ccccc} 0 & 0 & 0 & 0\\ 0& 80 & 80 & 0\\ 0& 80 & 80 & 0\\ 0 & 0 & 0 & 0\\ \end{array} \right] \end{eqnarray*}](https://algorithm.joho.info/wp-content/ql-cache/quicklatex.com-9c1283c6c15e1771de2796a012d69e5c_l3.png)
関連ページ
PythonとOpenCVを用いて空間フィルタリングを実装する方法について以下ページで解説しています。

PythonとOpenCVを用いた画像処理全般については以下ページで解説しています。

他の画像処理アルゴリズムについては、以下ページでまとめています。




コメント