機械学習のアルゴリズム（原理）やプログラミング方法について入門者向けにまとめました。
機械学習とは？
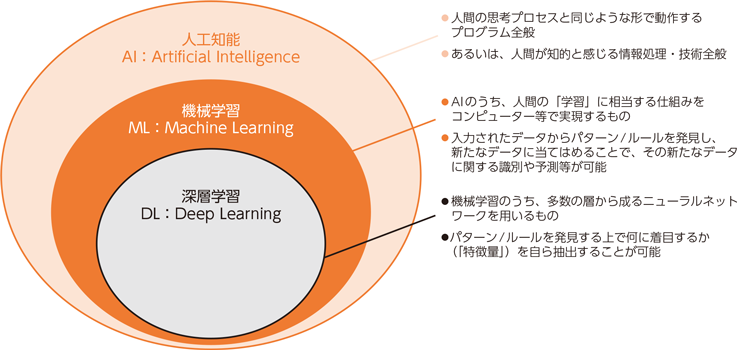
AI（人工知能）とは、「会話する」「画像を認識する」「意思決定する」といった「人間の知的活動を模倣する技術全般」を指します。機械学習（Machine Learning）とは、AIを実現するための手法の1つで、「人間が経験から学ぶ仕組みをコンピュータに学習させる技術」のことです。また、深層学習は機械学習の中でも「特徴抽出も自動で行う高度な手法」のことです。）
・AIは「上位概念」
・機械学習はその中の「学習技術」
・深層学習は機械学習の中でも「特徴抽出も自動で行う高度な手法」
活用事例や基本用語など、詳細は以下ページで別途解説しています。
また、機械学習の手法は「教師あり学習」「教師なし学習」「強化学習」の3つに分類されます。
| 学習タイプ | 正解ラベル | 主な目的 | 代表例 | 評価方法 |
|---|---|---|---|---|
| 教師あり学習 | あり | 予測・分類 | 回帰・分類モデル | 精度・誤差 |
| 教師なし学習 | なし | 構造発見 | クラスタリング・次元削減 | 可視化・統計指標 |
| 強化学習 | なし（報酬） | 最適行動選択 | Q学習・DQNなど | 累積報酬 |
上記の詳細は、以下ページで別途解説しています
回帰分析
| 予測対象 | 学習タイプ | 可読性 | 並列処理 |
|---|---|---|---|
| 連続値 | 教師あり | ○ | ✕ |
回帰分析は、ある変数（目的変数）を、他の変数（説明変数）から予測するための手法です。たとえば、「広告費（説明変数）」から「売上（目的変数）」を予測するようなケースです。また、回帰分析では、予測対象は「数値的な連続値」となります。つまり、目的変数（予測対象）が以下のような「量的データ」である必要があります。
- 売上金額（例：¥12,345）
- 気温（例：23.5℃）
- 身長（例：170.2cm）
- 時間（例：3.75時間）
もし目的変数（予測対象）が以下のような定性データであれば、一般的に回帰分析ではなく分類モデルを作成する学習手法を用います。
- 「はい／いいえ」
- 「猫／犬／鳥」
- 「A／B／Cクラス」
ただし、名前に「回帰」とついていますが、ロジスティック回帰は分類モデルです。回帰分析はいくつか種類がありますが、代表的なものは以下のとおりです。（リンクをクリックすると、各手法の解説ページに飛びます）
| 回帰の種類 | 説明 | 使用例 |
|---|---|---|
| 単回帰分析 | 説明変数が1つだけの回帰分析 | 気温からアイスの売上を予測 |
| 重回帰分析 | 説明変数が複数ある回帰分析 | 広告費・季節・競合状況から売上を予測 |
| 線形回帰 | 目的変数と説明変数の関係が直線で表される | 価格と需要の関係 |
| 非線形回帰 | 関係が曲線や指数関数など、非線形で表される | 成長曲線、人口増加など |
| リッジ回帰・ラッソ回帰 | 過学習を防ぐために正則化項を加えた回帰手法 | 多数の説明変数がある場合 |
| ロジスティック回帰 | 目的変数がカテゴリ（例：成功/失敗）の場合に使う分類モデル | メールがスパムかどうかの判定 |
ロジスティック回帰
| 予測対象 | 学習タイプ | 可読性 | 並列処理 |
|---|---|---|---|
| 分類 | 教師あり | ○ | ✕ |
- 特徴
- 線形回帰の出力をロジット関数に変換
- 対数オッズを重回帰で予測し、ロジット変換で確率を算出
- 尤度関数を目的関数に使用
- 原理の解説ページ
- 実装方法の解説ページ
サポートベクターマシン（SVM）
| 予測対象 | 学習タイプ | 可読性 | 並列処理 |
|---|---|---|---|
| 分類 | 教師あり | ○ | ✕ |
- 特徴
- マージン最大化により汎化性能が高い
- スラック変数で誤分類を許容
- カーネル法で非線形分離を可能に（カーネルトリックで計算量削減）
- 原理の解説ページ
- 実装方法の解説ページ
決定木
| モデル | 学習タイプ | 予測対象 | 可読性 | 並列処理 |
|---|---|---|---|---|
| 木構造 | 教師あり | 分類 | ○ | ✕ |
- 特徴
- 説明変数と閾値で条件分岐を繰り返す
- ジニ不純度やエントロピーで分岐条件を決定
- スケーリング不要・説明が容易
- 実装方法の解説ページ
ランダムフォレスト
| モデル | 学習タイプ | 予測対象 | 可読性 | 並列処理 |
|---|---|---|---|---|
| 木構造 | 教師あり | 分類 | ○ | ✕ |
- 特徴
- 決定木＋バギング（多数決で予測）
- 過学習の抑制・前処理が少ない
- 安定した精度・ハイパーパラメータ調整が可能
ニューラルネットワーク（多層パーセプトロン）
| モデル | 学習タイプ | 予測対象 | 可読性 | 並列処理 |
|---|---|---|---|---|
| 神経回路 | 教師あり | 連続値・分類 | ✕ | ○ |
- 特徴
- 入力・中間・出力の3層構造
- バックプロパゲーションによる学習
- 過学習しやすいが複雑なモデル構築が可能
- 原理の解説ページ
- 実装方法の解説ページ
深層学習（ディープラーニング）
特性
| モデル | 学習タイプ | 予測対象 | 可読性 | 並列処理 |
|---|---|---|---|---|
| 神経回路 | 教師あり | 連続値・分類 | ✕ | ○ |
- 特徴
- ディープニューラルネットワークを使用
- 複雑なモデル構築が可能
- 多くのハイパーパラメータ・過学習・勾配消失問題あり
- 原理の解説ページ
- 実装方法の解説ページ
階層型クラスタ分析
教師なし学習で、類似するデータをグループ化。クラス分類とは異なる。
| 予測対象 | 学習タイプ | 可読性 | 並列処理 |
|---|---|---|---|
| 分類 | 教師なし | ○ | ✕ |
- 特徴
- ユークリッド距離＋ウォード法が代表例
- 距離定義に基づきクラスタリング
- クラスタ数は後から変更可能
非階層型クラスタ分析
| 予測対象 | 学習タイプ | 可読性 | 並列処理 |
|---|---|---|---|
| 分類 | 教師なし | ✕ | ○ |
- 特徴
- k平均法が代表例
- クラスタ数は事前に指定（変更不可）
- 初期値により結果が変動
- 原理の解説ページ
- 実装方法の解説ページ
正則化
過学習を防ぐために、モデルの複雑さを抑える手法。パラメータのノルムを制限することで汎化性能を向上。
代表的手法
– LASSO正則化：特徴量選択が自動で行われる
– Ridge正則化：ノルムを小さく保つ（特徴量選択はしない）
主成分分析(PCA)による次元削減
次元削減とは、できるだけデータの情報を失わずに、データの次元数を減らすことです。
機械学習では「構造抽出」「汎化能力の向上」「可視化」「メモリ節約」などに活用されます。
代表例として主成分分析(PCA)があります。
- 特性
- 線形の次元削減を行う手法
- 特徴
- 寄与率を計算することで、各成分の重要度がわかる
- 主成分を計算することで、各成分の意味を推測できる
- 原理
トピックモデル
| 予測対象 | 学習タイプ | 可読性 | 並列処理 |
|---|---|---|---|
| 分類 | 教師なし | ✕ | ○ |
- 特徴
- 代表例はLDA
- トピック数（分類数）は事前に与える必要あり
- トピック毎の出現頻度からスコアを計算してデータを分類
- 計算量が大きい
強化学習
強化学習（Reinforcement learning）とは、エージェントがある環境内で現在の状態を観測し、収益を最大化するための取るべき行動を決定する学習手法の１つです。 つまり、エージェントが試行錯誤を繰り返していき、徐々に環境に適応した行動を取るような学習を行います。
- 特徴
- 試行錯誤を繰り返し「評価値（報酬）が最大となる行動」を学習
- 実装方法の解説ページ
関連ページ
- プログラミング
- コンピューター
- 情報処理系の資格試験対策
- 電気系の資格試験対策