この記事では、重回帰分析の意味や使い方、相関係数(偏回帰係数)や決定係数などについて解説します。
重回帰分析とは
重回帰分析とは、以下のようなモデル(式)を用いて予測する手法です。
(1) ![]()
| パラメータ | 説明 |
|---|---|
| 目的変数(予測値) | |
| y | 目的変数(観測値) |
| 説明変数(目的変数と相関のある観測値) | |
| 相関係数(重み、偏回帰係数) | |
| 切片(定数) |
相関係数(重み)は、目的変数が各説明変数に対してどのくらい影響を及ぼすかを示します。
単回帰分析の説明変数が複数になったものが「重回帰分析」です。
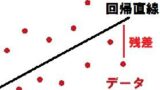
単回帰分析とは?計算式や例をわかりやすく解説
単回帰分析の式と意味原理、求め方、相関係数、決定係数、例題などについてわかりやすく解説します。
説明変数が複数になったので、単回帰よりも正確なモデルを立てやすくなります。
単回帰分析の流れは次の通りです。
手順
| – | 説明 |
|---|---|
| 1 | 目的変数と説明変数の観測値のセット |
| 2 | |
| 3 | 求めた重回帰直線の式を決定係数Rで評価する。 |
| 4 | 評価の結果が良ければ生成したモデル(単回帰直線の式)に説明変数の観測値を |
重回帰分析の例
重回帰の式のイメージを掴むために、地価の予測を例に考えてみます。
式
地価=重み1×最寄り駅までの距離 + 重み2×最寄りスーパーまでの距離 + 定数
| パラメータ | 内容 |
|---|---|
| 目的変数 | 地価 |
| 説明変数 | 最寄り駅までの距離、最寄りスーパーまでの距離 |
| 相関係数 | 重み1(立地条件が地価に与える影響) |
| 切片(定数) | その他の要因からなる数値(治安状況、景気の影響など) |
決定係数R2
単回帰分析と同様、決定係数![]() により求めた回帰直線がどの程度優れているか調べることができます。
により求めた回帰直線がどの程度優れているか調べることができます。
決定係数![]() は予測値の分散
は予測値の分散![]() と観測値yから以下の計算式により求まります。
と観測値yから以下の計算式により求まります。
(2) ![]()
決定係数![]() は0~1の値を取り、1に近づくほど精度が良いことを示します。
は0~1の値を取り、1に近づくほど精度が良いことを示します。
https://algorithm.joho.info/machine-learning/tutorial-ml/
https://algorithm.joho.info/machine-learning/tutorial-statistics/



コメント