単回帰分析の式と意味原理、求め方、相関係数、決定係数、例題などについてわかりやすく解説します。
単回帰分析とは
単回帰分析とは、以下のようなモデル(式)を用いて予測する手法です。
単回帰直線の式
(1) ![]()
| 変数 | 説明 |
|---|---|
| 目的変数(予測値) | |
| y | 目的変数(観測値) |
| x | 説明変数(目的変数と相関のある観測値) |
| a | 相関係数(重み、回帰係数) |
| b | 切片(定数) |
相関係数(重み)は、目的変数が説明変数に対してどのくらい影響を及ぼすかを示します。
手順
単回帰分析の流れは次の通りです。
| – | 説明 |
|---|---|
| ① | 目的変数と説明変数の観測値のセット(x, y)を用意する。 |
| ② | (x, y)から最小二乗法で単回帰直線の式を求める。 |
| ③ | 求めた単回帰直線の式を決定係数Rで評価する。 |
| ④ | 評価の結果が良ければ生成したモデル(単回帰直線の式)に説明変数の観測値をxに入れて予測値 |
単回帰分析の例
単回帰の式のイメージを掴むために、地価の予測を例に考えてみます。
式
地価=重み1×立地条件 + 定数
| パラメータ | 項目 |
|---|---|
| 目的変数 | 地価 |
| 説明変数 | 立地条件 |
| 相関係数 | 重み1(立地条件が地価に与える影響) |
| 切片(定数) | 立地条件以外の要因からなる数値(治安状況、景気の影響など) |
回帰直線の求め方
単回帰分析では、まずデータの散布図から回帰直線を求めます。
回帰直線は観測データ(x, y)の各点との残差が最も小さくなるようにします。
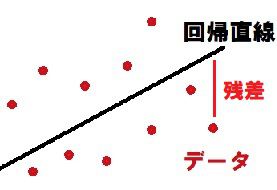
各点の残差の合計が最も小さくなるように直線を求めるために「最小2乗法」を用います。
最小2乗法では、傾きa(相関係数、重み)と切片bを以下の式で求めます。
(2) 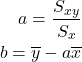
| 変数 | 説明 |
|---|---|
事前に用意したデータセット![]() から
から![]() 、
、![]() を求めます。
を求めます。
それが求まれば![]() も計算でき、単回帰直線の式が求まります。
も計算でき、単回帰直線の式が求まります。
決定係数(寄与率)
決定係数(寄与率)とは、単回帰の式の正当性を確かめるための指標です。
回帰式がどのくらい実際のデータ全体に対して近いのかを示すために決定係R数を計算します。
決定係数Rは0から1の値をとります。
全データが回帰直線の近くにあるほど1に近づきます。
寄与率は単に決定係数をパーセント表示にしたものです。(決定係数1=寄与率100%)
決定係数Rが1(寄与率が100%)に近いほど、回帰直線は説明力のあるものであるといえます。
(3) ![]()
つまり
決定係数は「1-(偏差の平方和)/(偏差の全平方和)」で計算できます。
| – | 関連記事 |
|---|---|
| 1 | 【機械学習入門】アルゴリズム&プログラミング |
| 2 | 【統計学入門】アルゴリズム&プログラミング |

コメント