構造力学における断面二次モーメントとは?計算式と例題について紹介します。
【断面二次モーメント】断面形状の曲げモーメントに対する硬さ(たわみの大きさ)
断面二次モーメントとは、「梁の曲げや変形に関わる係数」となります。
つまり、断面形状の曲げモーメントに対する「変形しにくさ=たわみの大きさ」を表します。
部材の曲げにくさは、材料の性質(鉄とかアルミとか木材とか)と形状(H型、I型、L型など)で決まり、断面二次モーメントは後者の指標となります。
一例として、鉄骨構造として多用されるH型鋼は、H字の縦棒に相当するフランジ部分に断面を集中させることにで断面二次モーメントを向上させています。
ある断面の全面積をA、断面内の微小な領域をdAとします。また、dAの座標を(x,y)をします。
このとき、x軸に関する断面二次モーメント![]() 、y軸に関するx軸に関する断面二次モーメント
、y軸に関するx軸に関する断面二次モーメント![]() はそれぞれ以下の式で計算できます。
はそれぞれ以下の式で計算できます。
(1) 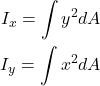
図心を求めるために計算していた断面一次モーメントの場合は基準座標系は気にしなくても良かったですが、断面二次モーメントはそれそのものを利用するため基準座標系が重要になります。
基準座標系によって、最終的に求められる断面の強度や剛性が異なりますので注意が必要です。
【並行軸の定理】任意の軸基準の断面二次モーメントを計算
並行軸の定理とは、図心基準以外の任意の軸基準の断面二次モーメントを求めるためのものです。
図中点線の長方形断面をx方向にx、y方向にy移動させた時のx軸に関する断面二次モーメント![]() 、y軸に関するx軸に関する断面二次モーメント
、y軸に関するx軸に関する断面二次モーメント![]() はそれぞれ以下の式で計算できます。
はそれぞれ以下の式で計算できます。
(2) 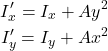
つまりは、図心基準の断面二次モーメントに移動距離の2乗と断面積Aを乗じたものを加算します。
H型、I型、L型などの複雑断面の断面二次モーメントを求めるのに重要な定理です。
【計算例】H鋼材

【部材断面】断面一次モーメント、断面二次モーメント、断面係数、断面二次半径の違いと計算式
構造力学における断面積、断面一次モーメント、図心、断面二次モーメント、断面係数、断面二次半径の違いと計算式と例題について紹介します。

構造力学・構造計算入門
構造力学の基礎、計算式、例題集について入門者向けにまとめました。

コメント