この記事では、Scilabクラウドで最終スライディングモード制御法のシミュレーションを行う方法についてソースコード付きで紹介します。
最終スライディングモード制御
スライディング制御法とは2つの制御入力を交互に切り換える制御の1つです。
H∞制御と比べるとマイナーですが、ロバスト性が高い制御法として知られています。
スライディングモード制御法には、切換超平面の設計法やコントローラの設計法によって種類があります。
今回は、Scilabクラウドを用いて、最終スライディングモード制御のシミュレーションを行ってみました。
●ソースコード
// 最終スライディングモード制御
L=[1 0; 0 1]; // 入力行列(アクチュエータに加わる力を表す行列)
k=10; //到達則のスカラ関数
m1=1; m2=1; //質量
k1=1; k2=2; //ばね定数
d1=1; d2=2; //減衰定数
M=[m1 0; 0 m2]; //
K = [k1 -k1; -k1 k1+k2];
D = [d1 -d1; -d1 d1+d2];
AF = [zeros(2,2) eye(2,2); -M*K -M*D];
BF = [zeros(2,2); L ];
// 平滑関数のパラメータ(チャタリング除去用)
P=4;
Q=1;
// 切換超平面Sの定義(極配置法で設計済)
S1=[4 0; 0 3];
S2=[eye(2,2)];
S = [S1 S2]; //切換超平面
// コンソールでフィードバックゲインの値を確認
F={L*inv(S*BF)*S*AF};
// 離散化
h = 0.02; // サンプリング時間
cont = syslin('c',AF,BF,S);
disc = dscr(cont,h);
[A,B,Sd] = abcd(disc);
// 初期値
X=[0.5 1.0 1.5 2.0]';
// シミュレーションループ
lines(0);
for i = 1:250;
// 外乱パラメータ
w=1;t=i;
// SMCの切換関数・制御入力・状態方程式
sigma = S*X;
U = -inv(S*BF)*{(S*AF*X)+Q*sign(sigma)+P*sigma};//等価制御入力
dX =A*X+B*U;//+[0; 0; 1 ; 1 ]*0.1*sin(w*t); //状態方程式
// データ格納
Xh1(:,i) = X;
Uh1(:,i) = U;
Sh1(:,i) = sigma;
X = dX;
end
// プロット
clf()
tt =0:h:(i-1)*h;
// グラフ描画
// 制御入力(第1象限)
subplot(222),plot(tt,Uh1(1,:),tt,Uh1(2,:)),xgrid(2)
title('制御入力')
xlabel('Time [s]')
ylabel('Control Input [N]')
// 状態変数(第2象限)
subplot(221),plot(tt,Xh1(1,:),tt,Xh1(2,:),tt,Xh1(3,:),tt,Xh1(4,:)),xgrid(2)
title('状態変数')
xlabel('Time [s]')
ylabel('Displacement [m]')
// 切換関数(第3象限)
subplot(223),plot(tt,Sh1),xgrid(2)
title('切換関数')
xlabel('Time [s]')
ylabel('Swiching Function')
// 位相平面(第4象限)
subplot(224),plot(Xh1(1,:),Xh1(3,:),Xh1(2,:),Xh1(4,:)),xgrid(2)
title('位相平面')
xlabel('x1')
ylabel('x2')
制御対象:2次のマスバネダンパ系
切換超平面:極配置法で設計済
コントローラ:最終スライディングモード制御
Scailab(クラウド版)を使えばWebブラウザ上で簡単に実行できます。
http://cloud.scilab.in/
実行結果
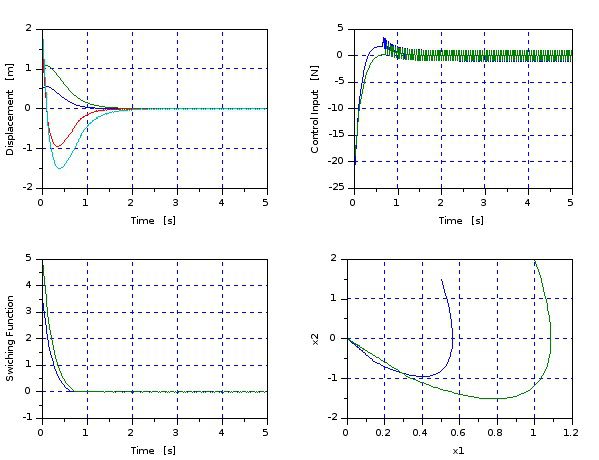
サンプルプログラムの実行結果です。
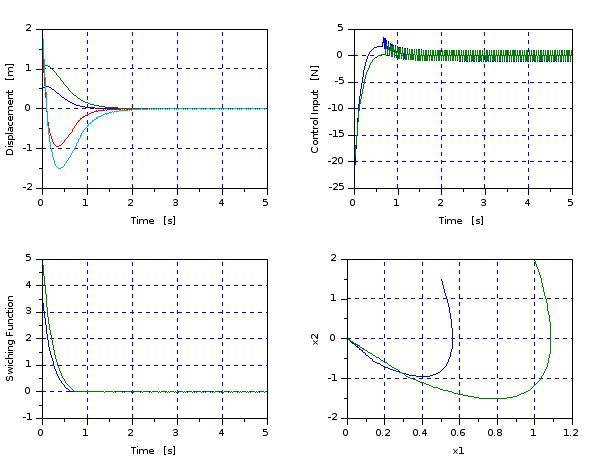
制御入力(第一象限):ギザギザになっているのは制御則を高速に交互に切換えているからです。
制御入力(第二象限):目標値0に収束させています。
429 Too Many Requests

コメント