【制御理論】状態方程式の同値変換

この記事では、状態方程式表現されたシステムの同値変換について紹介します。

同値変換

今回は、状態方程式の同値変換してみたいと思います。

システムの状態方程式は以下のような式で表されます。

(1) $\begin{eqnarray*} \dot{x}(t)=Ax(t)+Bu(t) \end{eqnarray*}$

ここで次のような変数 $\xi$ を用いて、状態方程式を正則変換します。

(2) $\begin{eqnarray*} \xi (t)=Tx(t) \end{eqnarray*}$

(Tは任意の正則行列)

上式を用いて、状態方程式を $\xi$ で表すと

(3) $\begin{eqnarray*} \dot{\xi}(t)&=&T\dot{x}(t)=T[Ax(t)+Bu(t)]\\ &=&TAT^{-1}\xi (t)+TBu(t) \end{eqnarray*}$

となります。同様に出力方程式も正則変換してやると

(4) $\begin{eqnarray*} y(t)=CT^{-1}\xi (t)+Du(t) \end{eqnarray*}$

が成り立ちます。正則変換した状態方程式と出力方程式を

(5) $\begin{eqnarray*} \tilde{A}&=&TAT^{-1}\\ \tilde{B}&=&TB\\ \tilde{C}&=&CT^{-1}\ \end{eqnarray*}$

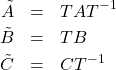
を用いて整理すると

(6) $\begin{eqnarray*} \dot{\xi}(t)=\tilde{A}\xi (t)+T\tilde{B}u(t)\\ y(t)=\tilde{C}T^{-1}\xi (t)+Du(t) \end{eqnarray*}$

で表せます。この式は、正則変換しても表現方法が変わるだけで、（単位が変わっただけのようなもの）システムの性質は変わらない（保存される）ことを意味します。例えば元の状態方程式が安定ならば、正則変換した状態方程式も安定になります。（固有値は不変）

これを元のシステムとは同値の関係にある（または単に同値である）といいます。