オプティカルフロー推定におけるLucasKanadeは?最小二乗法とガウシアンピラミッドによる推定の原理・計算式について解説します。
LucasKanade法とは
LucasKanade法は1981年にLucas、金出さんらによって作られたオプティカルフローを推定するアルゴリズムの1つです。LucasKanade法では、「最小二乗法」と「山登り法」を組み合わせることでより良いオプティカルフロー![]() の値を推定します。
の値を推定します。
| – | 説明 |
|---|---|
| ① | 最小二乗法でオプティカルフロー(移動物体の動きベクトル)を推定 |
| ② | 最小二乗法で求めた推定解は実際に使うと真値と大きくズレてしまう |
| ③ | 山登り法を使って推定解を真値に近づける |
前回記事
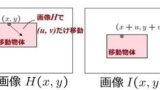
【最小二乗法】オプティカルフロー推定
1画素あたりの拘束方程式は1つであるため、このままではオプティカルフロー![]() を一意に求めることが出来ません。
を一意に求めることが出来ません。
そこで、LucasKanade法では「近い画素も同じ動きをする」 という仮定を用いることで、方程式の個数を増やし、解![]() を推定します。
を推定します。
例
画像I上の隣接し合う2点![]() が同じ動きをすると仮定すれば、下式のようにその2点の画素に対する拘束式の
が同じ動きをすると仮定すれば、下式のようにその2点の画素に対する拘束式の![]() は同じになります。
は同じになります。
(1) ![]()
よって、この2式を連立して解けば、未知数が2個、方程式も2個なので![]() を一意に求めることができます。
を一意に求めることができます。
これがLucasKanade法の基本的な考え方です。
ところが、実際には隣接する2点だけでなく、もっと広い領域で動きが同じであると仮定します。
例えば![]() の画素の動きがすべて同じだとすれば,下記のような9つの方程式が得られます。
の画素の動きがすべて同じだとすれば,下記のような9つの方程式が得られます。
(2) 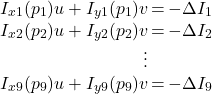
この場合,未知数2個、方程式9個となります。よって、9つの方程式を満たす2つの未知数![]() は一意に求めることができません。
は一意に求めることができません。
これをグラフに表すと下画像のようになります。
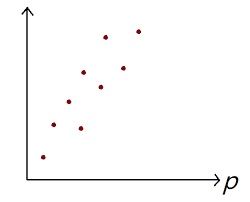
未知数が求まらないというのは、上のグラフで説明すると9つの点を通る直線は存在しないということです。
しかし、9つの点は全く散らばっているわけではありません。 (近い点同士なので画素の動きは似ている)
よって,9つの方程式を近似的に満足する未知数uとvは求めることができるはずです。
この事を先程のグラフで書き表すと下のような近似直線を求めることになります。
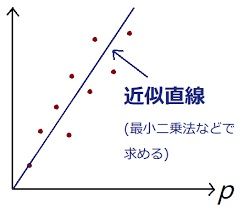
この近似直線を求める作業が、最初に述べた「最小二乗法」です。
このように「最小二乗法」を利用してオプティカルフローを推定することが「LucasKanade法」の基本的な考え方の1つです。
次の項目では、この流れを数式(線形代数)でまとめます。
先程の最小二乗法によってオプティカルフロー![]() を推定する一連の流れを線形代数の式で表していきます。
を推定する一連の流れを線形代数の式で表していきます。
![]() 個の画素が同じ動きをすると仮定すれば、つぎの
個の画素が同じ動きをすると仮定すれば、つぎの![]() 個のオプティカルフロー拘束式が得られます。
個のオプティカルフロー拘束式が得られます。
(3) 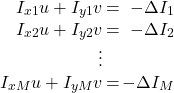
ただし
(4) 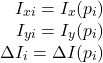
M個の方程式を1つの線形方程式にまとめると次のようになります。
(5) ![]()
ただし
(6) 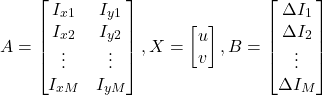
このとき,以下の定理を用いればオプティカルフローを推定することが出来ます。
定理
(5)式に対して次式を解けば![]() の近似値を求めることができます。
の近似値を求めることができます。
(7) ![]()
ただし
(8) ![]()
つまり、![]() の逆行列が存在すれば、最小二乗解(オプティカルフローの推定値)が一意に求まります。
の逆行列が存在すれば、最小二乗解(オプティカルフローの推定値)が一意に求まります。
また、線形代数の特性より、以下のようにして得られた解が良いか悪いかを調べることが出来ます。
| – | 説明 |
|---|---|
| ① | |
| ② | |
| ③ |
![]() を見てやるだけで簡単に解の安定性を調べることが出来ます。それにより、その画素が追跡しやすいか否かがわかり、特徴追跡をおこなうときに役立ちます。(
を見てやるだけで簡単に解の安定性を調べることが出来ます。それにより、その画素が追跡しやすいか否かがわかり、特徴追跡をおこなうときに役立ちます。(![]() の大きい点,つまり特徴点だけを抽出)
の大きい点,つまり特徴点だけを抽出)
物体追跡で一番大事なことは、追跡対象を選択することです。よって![]() の大きい点を対象に選べば
の大きい点を対象に選べば
安定的に追跡できることになります。
線形代数で表現することで、現代制御理論のように簡単に安定判別ができます。
計算例
隣接しあう3つの画素の動きが全く同じであるとし、以下の3つのオプティカルフロー拘束式が得られたとします。
(9) 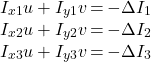
ただし,![]() ,
,
![]() とします。
とします。
このとき,線形方程式の定数行列![]() と行列
と行列![]() はつぎのようになる
はつぎのようになる
(10) 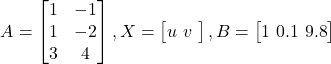
![]() となるので,(1)式で最小二乗解Xを求めることができます。
となるので,(1)式で最小二乗解Xを求めることができます。
(11) ![]()
よって画素の移動量は![]() となります。
となります。
【問題点】最小二乗法だけでは計算精度が悪い
オプティカルフロー拘束式は、以下の仮定①②の下で成立するものでした。
| – | 説明 |
|---|---|
| 仮定① | 移動前後で追跡したい点の画素値は変化しない |
| 仮定② | 追跡したい点の移動量は小さい(<1画素) |
しかし、当然ながら現実の世界では,これらの仮定はほとんど成立しません。
特に仮定②は成立しない場合がほとんどでしょう。(移動物体は1フレームで1画素以上移動することが多い)
仮定②が成立しない中でも最小二乗法でオプティカルフローを推定することができますが、その解は真値と大きくズレてしまいます。
そこで、最小二乗法だけでなく「山登り法」という方法を用いて仮定②が成立しない場合でもオプティカルフローを正確に推定します。
「山登り法」については次の項目で紹介します。
【山登り法】大きい移動量も精度良く推定
先程の項目でも紹介しましたが、オプティカルフロー拘束式は以下の2つの仮定で成立します。
| – | 説明 |
|---|---|
| 仮定① | 移動前後で追跡したい点の画素値は変化しない |
| 仮定② | 追跡したい点の移動量 |
しかし、![]() が大きい場合は仮定②が崩れてしまい、推定解が真値と大きくズレてしまいます。
が大きい場合は仮定②が崩れてしまい、推定解が真値と大きくズレてしまいます。
ここで、もし![]() の近似解
の近似解![]() が得られ、かつその精度が良ければ万々歳です。これを数式で表すと次のようになります。
が得られ、かつその精度が良ければ万々歳です。これを数式で表すと次のようになります。
(12) ![]()
ここで
(13) ![]()
とおくと、u,vは
(14) ![]()
と表せます。このとき、仮定1)より
(15) 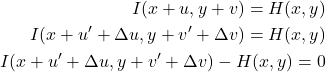
(16) ![]()
という方程式が得られます。この式は下式のオプティカルフロー拘束式とよく似ています。
(17) ![]()
よって、近似解![]() が得られれば、最小二乗法で
が得られれば、最小二乗法で![]() が推定でき、真値に近い
が推定でき、真値に近い![]() が計算できます。
が計算できます。
あとは近似解![]() をどのように求めるかが課題となります。そこで登場するのが「山登り法」です。
をどのように求めるかが課題となります。そこで登場するのが「山登り法」です。
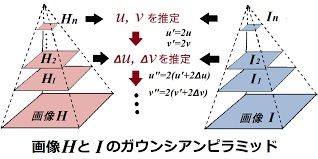
「山登り法」では、近似解![]() を求めるために、下図のような多重解像度画像のピラミッド(通称ガウンシアンピラミッド)を用いられます。
を求めるために、下図のような多重解像度画像のピラミッド(通称ガウンシアンピラミッド)を用いられます。
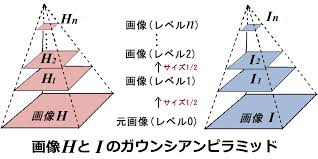
このピラミッドは画像![]() を元の解像度(一番下)から1/2ずつ小さくした画像を重ねています。
を元の解像度(一番下)から1/2ずつ小さくした画像を重ねています。
このように解像度を落とすことで、画素を物理的に大きくし、強引に仮定②を満足させます。
例えば![]() の画像ついて考えると下図のようになります。
の画像ついて考えると下図のようになります。
※赤色:移動物体
■元の解像度・・・移動量は2[px]
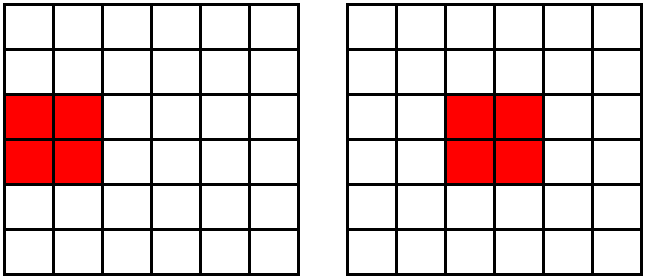
■解像度1/2・・・移動量は1[px]
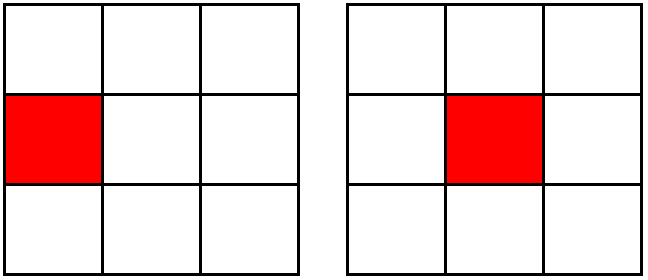
このように解像度を落とし続ければ、いずれ画素の移動量が1以下になり仮定2を満たせるので、拘束式を解いてオプティカルフローが求まります。このオプティカルフローが近似解![]() となります。
となります。
この近似解を使って、解像度が一段上の画像でまた近似解を求めます。この作業を元画像の解像度まで繰り返し行うことで、最終的に真値に近いオプティカルフローを求めることが出来ます。これが山登り法です。
LucasKanade法の流れまとめ
LucasKanade法の処理の流れをまとめると以下のようになります。
| – | 説明 |
|---|---|
| 1 | 画像 |
| 2 | 最初に, すべての画素における移動量の近似解を |
| 3.1 | |
| 3.2 | 各画素の移動量 |
| 3.3 | 解像度のレベルが一段高い画像 ① ②それ以外の画素に対して、隣(上下左右)の ③カウント変数を更新します。 |
| 4 |
Python版OpenCVによる実装例
Python版OpenCVによる実装方法を以下ページで解説しています。

関連ページ


コメント
(2)式の所の説明の「例えば33(=9)の画素」って、どういう意味でしょう?
※匿名様
コメントありがとうございます。
「33」は「3×3」の誤りでございます。
訂正致しました。