【制御理論】状態方程式とは

この記事では、現代制御理論の最も基本的な内容である「状態方程式」について紹介します。

状態方程式の概要

状態方程式(State Equation)とは、制御工学の分野では「システムの入出力関係を表現する微分方程式」のことです。

また、システムを状態方程式に置き換えることを「モデル化(モデリング)」と言います。

現代制御理論では、この状態方程式と線形代数を使って時間領域でシステムの設計・解析を行ないます。

(古典制御理論では、伝達関数と複素解析を使って周波数領域でシステムの設計・解析)

一般的に、状態方程式は以下のような式で表します。

(1) $\begin{eqnarray*} \dot{x}(t)&=&Ax(t)+Bu(t)\\ y(t)&=&C(x)+Du(t)\\ u(t) &\in &R^r, y(t)\in R^m, x(t)\in R^n \end{eqnarray*}$

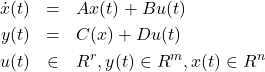
(1)式は状態方程式、(2)は出力方程式と呼ばれます。

また、 $u(t), y(t), x(t)$ はそれぞれ入力ベクトル、出力ベクトル、状態量ベクトルといいます。

そして、 $A$ はn次の正方行列、 $B, C, D$ は行列です。

nはシステムの次元(状態の次元)とも呼ばれ、 $n \geq r,m$ の関係が成り立ちます。これは入力がシステム内部(状態量)以下事しか操作できないことを示します。