【ニュートン法】アルゴリズム・プログラム

この記事では、ニュートン法のアルゴリズムとプログラムの実装方法について解説します。

ニュートン法

ニュートン法とは、数値計算的に方程式の近似解を求めるアルゴリズムの1つです。
つまり、f(x)=0になるxを求めることができます。

x=a1における接線f'(a1)はつぎのようになります。

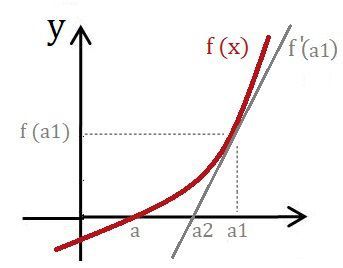
このとき、接線f'(a1)の切片a2は、a1よりも解aに近くなります。

次に、x=a2における接線f'(a2)はつぎのようになります。

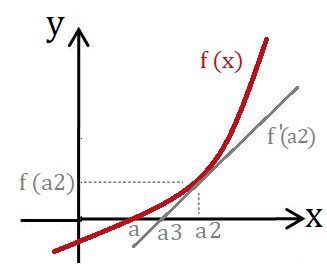
このとき、接線f'(a2)の切片a3は、a2よりも解aに近くなります。

この操作を繰り返すことで、解aにどんどん値が近づいていき近似解を求めることが出来ます。

この手順を繰り返せば繰り返すほど、算出される切片の値は目的となる値xに近づいていきます
ニュートン法では、次のような関数と接線の関係を利用して近似解を求めます。

先程の操作を数式にすると次のようになります。
接線f'(a1)は以下の式で表せます。

(1) $\begin{eqnarray*} a_2=a_1-\frac{f(a_1)}{f'(a_1)} \end{eqnarray*}$

同様に考えて

(2) $\begin{eqnarray*} a_3=a_2-\frac{f(a_2)}{f'(a_2)} \end{eqnarray*}$

これらを漸化式に直すと、

(3) $\begin{eqnarray*} a_{n+1}=a_n-\frac{f(a_n)}{f'(a_n)} \end{eqnarray*}$

となります。(nは計算回数)

つまり、計算回数nと初期値a1を与えると、近似解a_{n+1}を求めることができます。
初期値a1は適当な値を与えますが、解に近い値を与えるほど効率的に素早く近似解を求めることが出来ます。

プログラムで実装する場合は、計算回数nを指定するのでなく、収束条件を与えます。
近似解は解aに近づくと変化が小さくなります。

つまり、次のεの値が小さくなります。

(4) $\begin{eqnarray*} \epsilon= a_{n+1}-a_n \end{eqnarray*}$

プログラムでは、収束条件（εが一定値未満）になればニュートン法の繰り返し計算を終了します。
これにより、有効桁数が保証された近似解を求めることが出来ます。

プログラミングによる実装例は下記事で紹介しています。