DoM(Difference of Mean)の基本原理や計算式・特徴・例題についてまとめました。
DoMとは
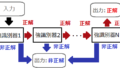
DoM(Difference of Mean)は、DoG(Difference of Gaussian)のガウシアンフィルタを平均値フィルタ(Mean filter)に置き換えたものです。つまり、異なるカーネルサイズの平均値フィルタを2つ用意し、平滑化された2つの画像の差分を取ることで輪郭画像を作成します。
利点としては、平均値フィルタは画素数の総和を求めるので、積分画像を用いた高速化が可能となります。
そのため、DoGと同じような処理を高速化して利用したい場合にDoMが用いられます。

解説動画
DoMフィルタの仕組み
平均値フィルタ(Mean Filter)は次のように計算されます。
$$ M_k(x, y) = \frac{1}{k^2} \sum_{i=-\frac{k}{2}}^{\frac{k}{2}} \sum_{j=-\frac{k}{2}}^{\frac{k}{2}} I(x+i, y+j) $$
ここで、$ I(x, y) $は座標$x, y$における画像の画素値、$ k $はカーネルサイズを表します。例えば、カーネルサイズが3×3の場合、$ k = 3 $ となります。
DoMフィルタは、異なるカーネルサイズ $ k_1 $ と $ k_2 $ で計算された平均値フィルタの差分を取ります。
$$ DoM(x, y) = M_{k_2}(x, y) – M_{k_1}(x, y) $$
$k_1$は高周波成分(エッジや細かいディテール)を強調するために小さめに設定します。一方、$k_2$は低周波成分(なだらかな変化や大きな構造)を強調するために大きめに設定します。ただし、ーネルサイズが大きくなるほど、フィルタ処理に時間がかかります。特にリアルタイム処理が必要な場合は、適度なカーネルサイズを選ぶ必要があります。
適切なカーネルサイズは、以下のように輪郭の検出結果を見ながら調整を繰り返して見つけることが一般的です。
- $k_1$ を3×3、$k_2$ を5×5や7×7に設定して、フィルタ処理を行います。
- 出力画像を確認し、輪郭がどの程度強調されているか評価します。
- 必要に応じて、カーネルサイズを微調整します。輪郭が強すぎる場合は $k_1$ を大きくし、輪郭が弱すぎる場合は$k_2$を小さくします。
プログラミングによる実装例
プログラミングによる実装例は、以下ページで別途解説しています。

関連ページ



コメント