積分画像とは?計算方法と高速化の仕組みについてまとめました。
積分画像とは
積分画像(Integral Image)は、注目画素とその左と上にある全ての画素値の和を求めた物です。
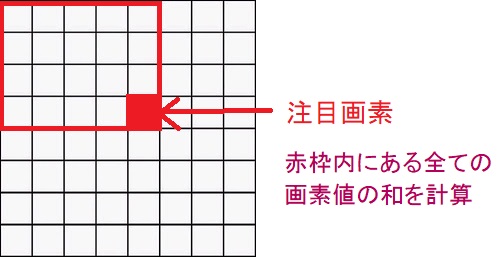
例えば、入力画像$I$が与えられた場合
$$ I= \left[ \begin{array}{ccc} I(0,0) & I(1,0) & I(2,0) \\ I(0,1) & I(1,1) & I(2,1) \\ I(0,2) & I(1,2) & I(2,2) \\ \end{array} \right] $$
積分画像$I’$の画素値は次のように計算します。
$$ I’= \left[ \begin{array}{ccc} I'(0,0) & I'(1,0) & I'(2,0) \\ I'(0,1) & I'(1,1) & I'(2,1) \\ I'(0,2) & I'(1,2) & I'(2,2) \\ \end{array} \right] $$
$$ \begin{aligned} I'(0,0) &= I(0,0)\\ I'(1,0) &= I(0,0) + I(1,0)\\ I'(2,0) &= I(0,0) + I(1,0) + I(2,0)\\ I'(0,1) &= I(0,0) + I(1,0)\\ I'(1,1) &= I(0,0) + I(1,0) + I(0,1) + I(1,1)\\ I'(2,1) &= I(0,0) + I(1,0) + I(0,1) + I(1,1) + I(2,0) + I(2,1)\\ I'(0,2) &= I(0,0) + I(0,1) + I(0,2)\\ I'(1,2) &= I(0,0) + I(0,1) + I(0,1) + I(1,0) + I(1,1) + I(1,2)\\ I'(2,2) &= I(0,0) + I(0,1) + I(0,1) + I(1,0) + I(1,1) + I(1,2) + I(2,0) + I(2,1) + I(2,2) \end{aligned} $$
解説動画
積分画像による高速化の仕組み
積分画像は近傍画素の処理の高速化によく使われます。
例えば、注目画素と8近傍の計9画素の画素値の総和を求めたいとします。
普通に計算すると、「画素値の取り出し9回」と「加算8回」を行う必要があります。
ところが、あらかじめ積分画像を作っておけば、「画素値の取り出し4回」と「加算1回+減算2回」で済ませることができます。
例として、赤色領域(注目画素+8近傍の画素)にある画素値の総和$S$を求めることを考えてみましょう。

$S$は以下の式で計算できます。
$$ S=S_1-S_2-S_3+S_4 $$
$S_1$から$S_2$と$S_3$を引き、引きすぎた分$S_4$を加算しています。
ここで、$S_1, S_2, S_3, S_4$は積分画像の画素値に等しくなります。
■積分画像$I’$

$$S_1=I'(3,3)\\ S_2=I'(0,3)\\ S_3=I'(3,0)\\ S_4=I'(0,0)$$
よって、積分画像を先に作成しておけば、少ない計算回数(加算1回+減算2回)と画素へのアクセス回数(4回)で画素値の総和を計算できます。
それにより計算時間を大幅に抑えることができます。
近傍画素の個数が多くなったり、繰り返し回数が増えるほど、高速化の効果も大きくなります。
積分画像を使った高速化は、畳み込み演算や特徴量の計算などでよく利用されている重要なアルゴリズムです。
積分画像の計算式
入力画像$I$とその積分画像$I’$があるとします。
このとき、左上座標$(x, y)$、幅$w$, 高さ$h$の矩形領域内にある画素値の総和$S$は次式で計算できます。
$$ S=I'(x+w,y+h)-I'(x,y+h)-I'(x+w, y)+I'(x,y) $$
関連ページ




コメント