HoG特徴量の基本的な原理や仕組みについてまとめました。
HoG特徴量とは
HoG(Histograms of Oriented Gradients)特徴量は、画像処理やコンピュータビジョンの分野でよく使われる手法です。
主に物体検出や画像認識に利用されます。
HoGとは、局所領域 (セル) の画素値の勾配方向をヒストグラム化したものです。そのヒストグラムを特徴量としたのが、Hog特徴量です。
勾配を特徴量としているため、画像スケールに対してロバストであるという優れた特徴があります。
画像のスケール(拡大や縮小)にに対してロバストであるということは、画像のサイズや解像度が変わっても、特徴量の抽出結果が安定していることを意味します。
例えば、ある物体が小さく写っている画像と大きく写っている画像があった場合、HoG特徴量を用いることで、どちらの画像でも同じ特徴を抽出できるため、物体認識の精度が向上します。これにより、異なる距離や視点から撮影された画像でも、同じ物体を正確に検出することが可能になります。
この特性は、物体検出や画像認識のアルゴリズムにおいて重要であり、応用例としては、顔検出や車両検出などがあります。
HoG特徴量の計算方法
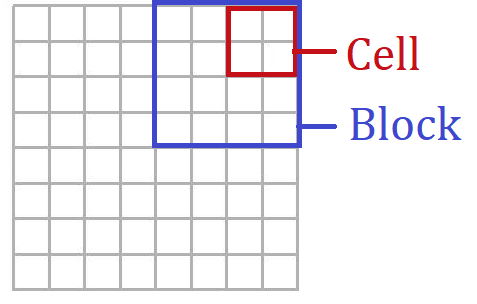
① 入力画像を複数のブロックに分割します。
また、各ブロックをセルに分割します。
■1ブロック($2\times 2$セル)、1セル($2\times 2$ピクセル)で分割する場合
② 入力画像$I$を微分します。
$$ I_{x}(x, y)=I(x+1,y)-I(x, y) $$
$$ I_{y}(x, y)=I(x, y+1)-I(x, y) $$
③ 微分画像から勾配強度$|I|$と勾配方向$\theta$を求めます。
$$ |I|=\sqrt{I_x^2+I_y^2} $$
$$ \theta = tan^{-1}\frac{I_y}{I_x}=atan2(I_y, I_x) $$
④ 勾配方向を9方向(0~180度まで20度ずつ)に量子化します。
⑤ セル毎に強度で重みを付けて勾配方向ヒストグラムを計算します。
⑥ 各ブロック内のヒストグラムを正規化し、特徴量を計算します。正規化により、照明変化やコントラスト変化に対してロバストになります。
$$ h(n)=\frac{h(n)}{H}$$
ここで、$h(n)$はn番目の勾配方向ヒストグラムです。分母$H$は1ブロックのHOG特徴量の総和で次式で計算します。
$$ H=\sqrt{(\sum_{k=1}^{m\times m\times N}h(k)^2)+\epsilon} $$
$m$はセルサイズ、$N$は勾配方向数、$\epsilon =1$です。
⑦ 全てのヒストグラムを結合すればHoG特徴量の完成です。
関連ページ





コメント