【画像処理】フーリエ変換の原理・実装例

この記事では、画像処理におけるフーリエ変換について解説します。

画像処理におけるフーリエ変換

フーリエ変換は周波数解析ができる便利なデータ変換です。
画像に対しても利用できます。

–	フーリエ変換の基本に関してはこちら
①	フーリエ変換の原理・意味
②	逆フーリエ変換の原理・意味
③	離散フーリエ変換(DFT)の原理・意味
④	高速フーリエ変換(FFT)の原理・意味
⑤	【フーリエ変換】サンプリング周波数とナイキスト周波数の関係性・違い

ただし、周波数の考え方が通常の信号とは異なるので注意する必要があります。

種類	説明
通常の信号	周波数=単位時間内にどのくらい振動するか
画像	周波数=単位ピクセル内に画素値がどのくらい変化するか

つまり、画像の場合、1[px]移動したときの画素値の変化が激しいほど、高周波となります。
このため、画像処理でのフーリエ変換は「時間領域→周波数領域」ではなく「空間領域→空間周波数領域」となります。

画像データは2次元であり、水平方向と垂直方向の2つの空間周波数成分を持っています。
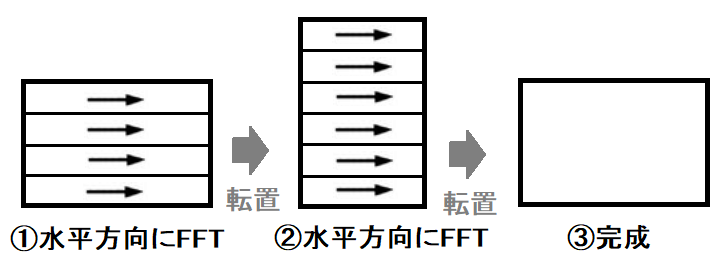
画像データに対する2次元FFTは次の手順で行います。

–	説明
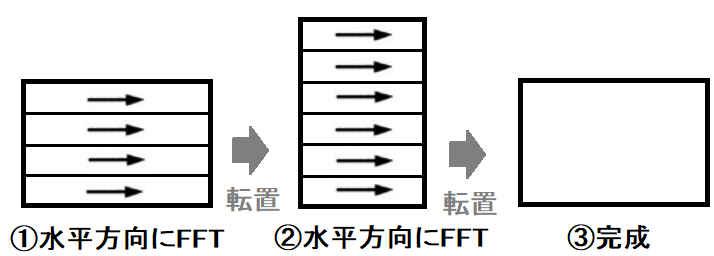
①	画像データの水平方向に1次元FFTを行います。
②	画像を転置し、再び水平方向に1次元FFTを行います。
③	もう１度画像を転置すれば完成です。

手順①～③で結果的に画像データに対して水平方向と垂直方向に1次元FFTを行うことになります。

ただし、FFTを利用するには画像の縦横それぞれの大きさが2の冪乗である必要があります。

画像の振幅スペクトル

振幅スペクトルとは

画像データに対して2次元FFT(手順①～③)を行うと次のような振幅スペクトルが得られます。

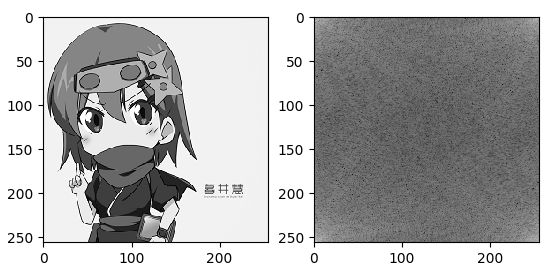
※プロ生ちゃんの画像をお借りして入力しました。

この振幅スペクトルは、中心から離れるに従って低周波数成分になるスペクトルで、画像データの周波数分布を表します。
画素値が大きい（白っぽい）ほど、その周波数成分が多く含まれていることになります。
つまり、中心付近に白い画素が集中するほど画像に高周波成分が多く含まれることを意味します。
（逆に、四隅付近に集中すれば低周波数成分が多く含まれる）

このように画像の振幅スペクトルからも（空間）周波数成分の解析ができます。

周波数領域の入れ替え

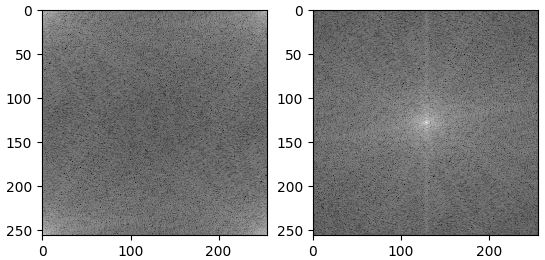
振幅スペクトルを利用する場合、第1象限と第3象限、第2象限と第4象限を入れ替えて利用するのが一般的です。
その際、中心から離れるに従って高周波数成分となるスペクトルへ変換されます。
入れ替えにより、後述する空間周波数フィルタリングを簡単に行うことができるようになります。

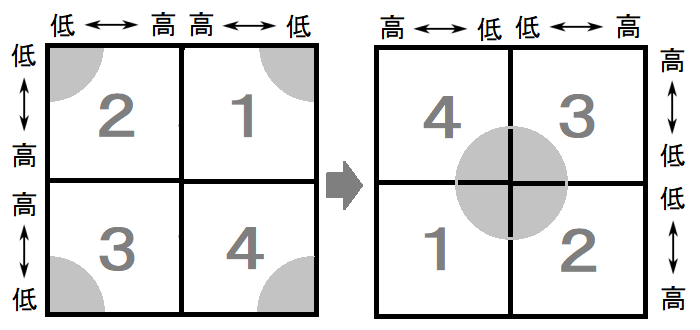
■入れ替えた例

空間周波数フィルタリング

空間周波数フィルタリングでは、画像から特定の周波数成分のみを取り出します。
代表的なものは「ローパスフィルタ」「ハイパスフィルタ」「バンドパスフィルタ」です。

フィルタリングの種類

–	説明	利用例
ローパスフィルタ	低周波数成分のみを通過させるフィルタ	画像のノイズ除去など
ハイパスフィルタ	高周波成分のみを通過させるフィルタ	画像の輪郭、特徴点抽出など
バンドパスフィルタ	特定範囲の周波数成分のみを通過させるフィルタ	画像のデータ圧縮など（見た目の影響が少ない成分を除去）

フィルタの設計例

周波数領域の象限を入れ替えることで次のように空間周波数フィルタリングを簡単に行うことができます。

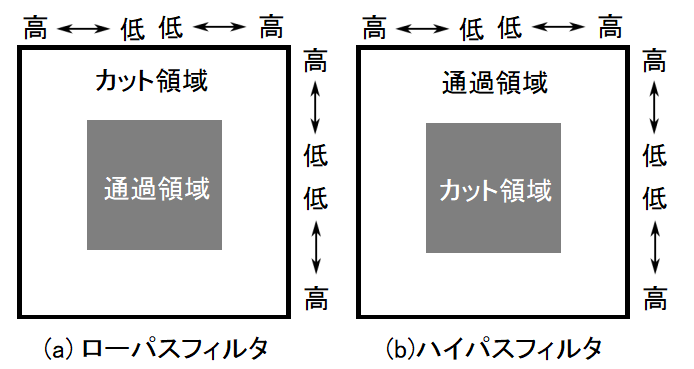
ローパスフィルタ(a)では、中心付近にある低周波数成分のみを通過させます。
一方、ハイパスフィルタ（b）では端の方にある高周波数成分のみを通過させます。
プログラムで実装する場合、カットする領域のスペクトルのみを0にします。

操作手順

空間周波数フィルタリングの基本的な操作手順は次の通りです。

–	説明
①	画像を2次元FFTします。
②	周波数領域を入れ替えます。
④	各種フィルタリングを行います。（例えばローパスフィルタならカット領域のスペクトルを0にします）
⑤	周波数領域を入れ替えます。(元に戻す)
⑥	2次元の逆FFTをします。
⑦	フィルタリングされた画像が完成します。