【画像処理】一次微分フィルタの原理・特徴・計算式

画像処理における1次微分フィルタの原理や特徴、計算式についてまとめました。

一次微分フィルタとは
一次微分フィルタのカーネル
【計算例】4×4の入力画像を一次微分フィルタに掛けた場合
プログラミングで実装

一次微分フィルタとは

一次微分フィルタは、画像から輪郭を抽出する空間フィルタです。
一次微分を計算することで、注目画素の左右・上下の画素値の変化の傾きが求まります。
画像の輪郭は画素値の変化が大きいため、微分した画素値が大きい箇所が輪郭となります。

■入力画像（左）、出力画像（右）

出力画像を見ると、輪郭の部分が白くなっている、つまり画素値が大きいことがわかります。

一次微分フィルタのカーネル

注目画素 $I(x, y)$ の水平方向、および垂直方向それぞれの一次微分 $I_{x}(x, y), I_{y}(x, y)$ は次のようになります。

(1) $\begin{eqnarray*} I_{x}(x, y)=I(x+1,y)-I(x, y)\\ I_{y}(x, y)=I(x, y+1)-I(x, y) \end{eqnarray*}$

よって、一次微分フィルタの水平方向微分のカーネル $K_x$ 、および垂直方向微分に用いるカーネル $K_y$ は次のようになります。

(2) $\begin{eqnarray*} K_x= \left[ \begin{array}{ccc} 0 & 0 & 0 \\ 0 & -1 & 1 \\ 0 & 0 & 0 \\ \end{array} \right], K_y= \left[ \begin{array}{ccc} 0 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 1 & 0 \\ \end{array} \right] \end{eqnarray*}$

ただし、このやり方だと、実際には2つの画素の中間における微分値（ $I_{x}(x+0.5, y), I_{y}(x, y+0.5)$ ）となってしまいます。
そこで、注目画素の両端の画素値の差分を計算することで、注目画素の位置に合わせる方法もあります。

(3) $\begin{eqnarray*} I_{x}(x, y)=I(x+1,y)-I(x-1, y)\\ I_{y}(x, y)=I(x, y+1)-I(x, y-1) \end{eqnarray*}$

このとき、水平方向微分のカーネル $K_x$ 、および垂直方向微分に用いるカーネル $K_y$ は次のようになります。

(4) $\begin{eqnarray*} K_x= \left[ \begin{array}{ccc} 0 & 0 & 0 \\ -1 & 0 & 1 \\ 0 & 0 & 0 \\ \end{array} \right], K_y= \left[ \begin{array}{ccc} 0 & -1 & 0 \\ 0 & 0 & 0 \\ 0 & 1 & 0 \\ \end{array} \right] \end{eqnarray*}$

水平方向微分では縦方向の輪郭を取り出すことができます。
逆に、垂直方向微分では横方向の輪郭を取り出します。

最後に、縦方向に検出された輪郭画像の画素値を $I_{x}(x, y)$ 、横方向に検出された輪郭画像の画素値を $I_{y}(x, y)$ とすると、縦横両方向の輪郭画像の画素値 $I'(x, y)$ は、次式で計算できます（二乗和平方根）。

(5) $\begin{eqnarray*} I'(x, y) = \sqrt{I_{x}(x, y)^2 + I_{y}(x, y)^2} \end{eqnarray*}$

【計算例】4×4の入力画像を一次微分フィルタに掛けた場合

入力画像 $I$ と一次微分フィルタ（垂直方向微分）のカーネル $K$ が次のように与えられたとき、出力画像 $I'$ を求めます。

(6) $\begin{eqnarray*} I= \left[ \begin{array}{ccccc} 0 & 0 & 0 & 0\\ 0& 10 & 10 & 0\\ 0& 0 & 10 & 0\\ 0 & 0 & 0 & 0\\ \end{array} \right], K= \left[ \begin{array}{ccccc} 0 & -1 & 0\\ 0 & 0 & 0\\ 0 & 1 & 0\\ \end{array} \right] \end{eqnarray*}$

入力画像 $I$ とカーネル $K$ を畳み込み演算してやると

(7) $\begin{eqnarray*} I'(1,1)&=&0\\ I'(2,1)&=&1\cdot 10=10\\ I'(1,2)&=&(-1\cdot 10)=-10\\ I'(2,2)&=&(-1\cdot 10)=-10\\ \end{eqnarray*}$

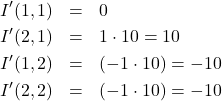
となります。今回、入力画像の端の画素値は0とします。
また、0未満の画素値は絶対値を取って10とします。

すると、出力画像 $I'$ は次のようになります。

(8) $\begin{eqnarray*} I'= \left[ \begin{array}{ccccc} 0 & 0 & 0 & 0\\ 0& 0 & 10 & 0\\ 0& 10 & 10 & 0\\ 0 & 0 & 0 & 0\\ \end{array} \right] \end{eqnarray*}$