【画像処理】最近傍補間法の原理・計算式

この記事では、画像を拡大・縮小・回転したときなどに利用する補間法の1つである「最近傍法補間法」の原理や計算方法についてまとめました。

最近傍法（Nearest neighbor）による画像拡大・縮小の仕組み
【計算例】2×2のグレースケール画像を1.5倍に拡大する場合
関連ページ

最近傍法（Nearest neighbor）による画像拡大・縮小の仕組み

最近傍法（Nearest neighbor・ニアレストネイバー法）は、画像を拡大した際に最近傍にある画素をそのまま使う線形補間法です。
単純なアルゴリズムなので、他の補間法と比較して処理速度が速い反面、画質が劣化しやすくなります。

最近傍法によって拡大後の画素値を求める計算式は以下のとおりです。

計算式

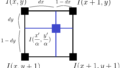
拡大前の元画像を $I$ 、拡大率 $\alpha$ で拡大後の画像を $I'$ とします。
このとき、拡大後の画素値は次の式で求めます。

(1) $\begin{eqnarray*} I'(x, y)=I([\frac{x}{\alpha}], [\frac{y}{\alpha}]) \end{eqnarray*}$

[]は四捨五入を表しています。
つまり、「拡大後の座標÷拡大率」を四捨五入して得られた座標にある元画像の画素値をそのまま利用します。

【計算例】2×2のグレースケール画像を1.5倍に拡大する場合

次のような入力画像 $I$ を1.5倍に拡大した画像 $I'$ について考えます。

(2) $\begin{eqnarray*} I= \left[ \begin{array}{ccccc} 50 & 100 \\ 150 & 200 \\ \end{array} \right] \end{eqnarray*}$

画像 $I$ のサイズは2×2なので1.5倍に拡大した画像 $I'$ は以下のように3×3のサイズとなります。

(3) $\begin{eqnarray*} I'= \left[ \begin{array}{ccccc} I'(0,0) & I'(1,0) & I'(2,0) \\ I'(0,1) & I'(1,1) & I'(2,1) \\ I'(0,2) & I'(1,2) & I'(2,2) \\ \end{array} \right] \end{eqnarray*}$

拡大後の画素値を最近傍法で求まると次のようになります。

(4) $\begin{eqnarray*} I'(0,0)=I([\frac{0}{1.5}], [\frac{0}{1.5}])=I(0,0)=50 \\ I'(1,0)=I([\frac{1}{1.5}], [\frac{0}{1.5}])=I(1,0)=100 \\ I'(2,0)=I([\frac{2}{1.5}], [\frac{0}{1.5}])=I(1,0)=100 \\ I'(0,1)=I([\frac{0}{1.5}], [\frac{1}{1.5}])=I(0,1)=150 \\ I'(1,1)=I([\frac{1}{1.5}], [\frac{1}{1.5}])=I(1,1)=200 \\ I'(2,1)=I([\frac{2}{1.5}], [\frac{1}{1.5}])=I(1,1)=200 \\ I'(0,2)=I([\frac{0}{1.5}], [\frac{2}{1.5}])=I(0,1)=150 \\ I'(1,2)=I([\frac{1}{1.5}], [\frac{2}{1.5}])=I(1,1)=200 \\ I'(2,2)=I([\frac{2}{1.5}], [\frac{2}{1.5}])=I(1,1)=200 \\ \end{eqnarray*}$