画像処理におけるLoGフィルタの原理・特徴・計算方法についてまとめました。
LoGフィルタとは
LoGフィルタ(Laplacian Of Gaussian Filter)とは、ガウシアンフィルタとラプラシアンフィルタを組み合わせたフィルタです。
ラプラシアンフィルタは二次微分で輪郭を検出するため、ノイズが強調されやすいという欠点があります。LoGフィルタでは、ガウシアンフィルタで画像を平滑化してノイズを低減した後、ラプラシアンフィルタで輪郭を検出します。これによりラプラシアンフィルタの欠点を抑えることができます。
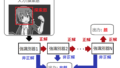
■ラプラシアンフィルタ(左)とLoGフィルタ(右)


解説動画
LoGフィルタの計算式
LoGフィルタの計算式は、ガウス関数のラプラシアン(2階微分)により求まります。
ガウス関数は以下のとおりです。
$$ G(x, y) = \frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}} $$
- $ G(x, y) $:座標 $(x, y)$ におけるガウス関数の値(フィルタの重み)。
- $ \sigma $:ガウス分布の標準偏差。値が大きいほど、平滑化の効果が大きくなり、フィルタの範囲が広がる。(その分、計算コストも高くなる)
- $ e $:自然対数の底 (約2.718) 。
この計算式のxについての一次微分を求めます。
$$ \frac{\partial G(x, y)}{\partial x} = \frac{\partial}{\partial x}\left( \frac{1}{2\pi\sigma^2}e{-\frac{x2+y2}{2\sigma^2}} \right) = \frac{1}{2\pi\sigma^2}\left( -\frac{x}{\sigma^2} \right)e^{-\frac{x^2+y^2}{2\sigma^2}} $$
さらに、上式をもう一度微分することで、二次微分を求めます。
$$ \frac{\partial^2 G(x, y)}{\partial x^2} = \frac{1}{2\pi\sigma^2}\left( \left( \frac{x^2}{\sigma^4} – \frac{1}{\sigma^2} \right)e^{-\frac{x^2+y^2}{2\sigma^2}} \right) $$
同様にして、yについても二次微分を求めます。
$$ \frac{\partial^2 G(x, y)}{\partial y^2} = \frac{1}{2\pi\sigma^2}\left( \left( \frac{y^2}{\sigma^4} – \frac{1}{\sigma^2} \right)e^{-\frac{x^2+y^2}{2\sigma^2}} \right) $$
x と y の二次微分の和を求めると、ラプラシアンが求まります。
$$ \nabla^2 G(x, y) = \frac{\partial^2 G(x, y)}{\partial x^2} + \frac{\partial^2 G(x, y)}{\partial y^2} $$
$$ = \frac{1}{2\pi\sigma^2}\left( \left( \frac{x^2 + y^2}{\sigma^4} – \frac{2}{\sigma^2} \right)e^{-\frac{x^2+y^2}{2\sigma^2}} \right) $$
上式を整理して、定数をまとめるとLoGフィルタの計算式が求まります。
$$ LoG(x, y)=\frac{x^2+y^2-2\sigma ^2}{2\pi \sigma ^6}e^{-\frac{x^2+y^2}{2\sigma ^2}} $$
関連ページ




コメント
-sigma^2 → -2*sigma^2
ご指摘ありがとうございます。
初歩的な質問なのですが、このフィルタって、【ログフィルタ】って読みますか?それとも【エルオージーフィルタ】って読みますか?
正しいのかわかりませんが、私はエルオージーと読んでました。
loGは、ログって読みますか?エルオージーで読みますか?
正しいのかわかりませんが、私はエルオージーと読んでました。