この記事では、画像処理における線形濃度変換の原理や仕組みについてまとめました。
線形濃度変換
本ページの内容は以下動画で解説しています。
線形濃度変換とは、横軸を入力画像の画素値、縦軸を出力画像の画素値とする線形マッピングです。
GIMPやPhotoshopなどの画像加工ソフトに濃度を変更するツールとして組み込まれています。
線形濃度変換は、画像のコントラストを調整し、画像を人が視認しやすいように変換することができます。
今回は、線形濃度変換の代表例をいくつか紹介します。
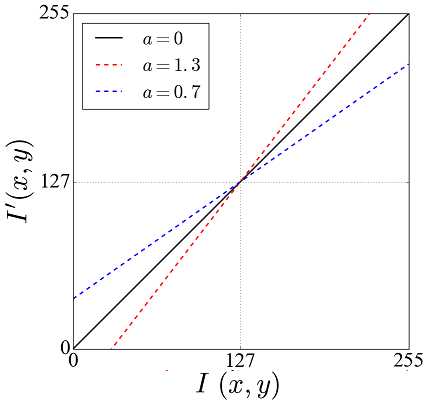
変換① 画素値をa倍
入力画像の画素値を![]() とすると、
とすると、![]() 倍した出力画像の画素値
倍した出力画像の画素値![]() は次式で計算できます。
は次式で計算できます。
(1) ![]()
| – | 説明 |
|---|---|
| a>1 | より明るくなり、コントラストも高くなる |
| a=1 | 変化なし |
| a<1 | より暗くなり、コントラストも低くなる |
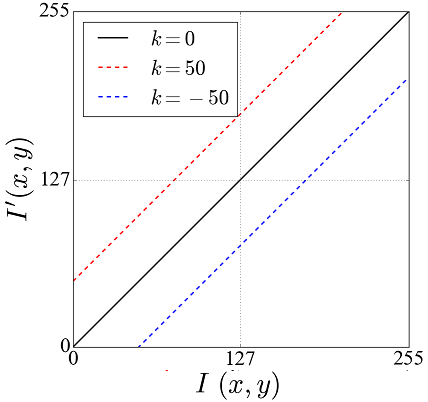
変換② コントラストを全体的に明るく・暗く
コントラストを全体的に「明るく」or「暗く」することを考えます。
入力画像の画素値を![]() とすると、出力画像の画素値
とすると、出力画像の画素値![]() は次式で計算できます。
は次式で計算できます。
(2) 
| パラメータ | 説明 |
|---|---|
| 全体的に明るくなる | |
| 全体的に暗くなる |
※![]() の絶対値が大きいほど効果も大きくなります
の絶対値が大きいほど効果も大きくなります
■グラフ描画用プログラム(Python)
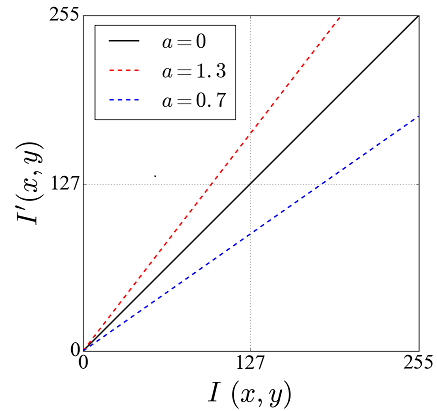
変換③ コントラストの強弱
入力画像の画素値を![]() とすると、コントラストの強弱を調整した出力画像の画素値
とすると、コントラストの強弱を調整した出力画像の画素値![]() は次式で計算できます。
は次式で計算できます。
(3) 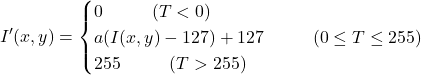
| – | 説明 |
|---|---|
| コントラストを強める | |
| コントラストを弱める |
変換④ ヒストグラムの拡張(伸張)
ヒストグラムの拡張(伸張)とは、画素値の分布が特定の範囲に偏っている場合に、広い範囲に拡張(伸長)する濃度変換です。
画素値の分布を![]() ~
~![]() の範囲に引き伸ばすとします。
の範囲に引き伸ばすとします。
このとき、入力画像の画素値を![]() とすると、出力画像の画素値
とすると、出力画像の画素値![]() は次式で計算できます。
は次式で計算できます。
(4) ![]()
ここで、![]() は入力画像の画素値の最大値です。
は入力画像の画素値の最大値です。
関連ページ
今回紹介した4つの線形濃度変換をPython版OpenCVで実装する方法について以下ページで解説しています。
https://algorithm.joho.info/programming/python/opencv-liner-histogram-stretching-py/

【画像処理超入門】アルゴリズムの仕組みと実装方法を簡単に解説
画像処理超アルゴリズムの仕組みとプログラミングによる実装方法を簡単に解説します。

コメント