極配置法で切換超平面の設計（スライディングモード制御）

この記事では、スライディングモード制御の切換超平面を極配置法で設計する方法を紹介します。

極配置法の概要
極配置法による切換超平面の設計
切換超平面の設計例(極配置法)

極配置法の概要

スライディングモード制御の切換超平面Sを設計する方法の1つに、状態フィードバック制御でもお馴染みの極配置法を用いる手法があります。
この設計法では、等価制御系（スライディングモードの状態にあるシステム）の極をすべて負に配置することで、状態を原点に収束させる切換超平面を実現させます。

ただし、設計するときには配置する極の数に注意する必要があります。
状態フィードバック制御における極配置では、制御対象の次数の数nだけ極を配置を行います。
例）3次系なら極3個

それに対し、切換超平面の設計における極配置では制御対象の次数から入力の数を引いた個数n-mだけ極を配置します。
例）4次系で2入力なら極2個
入力の数だけ少なくなる理由は、等価制御系の極を配置するからです。
（等価制御系とは切換超平面上を滑っているときのシステムのことで、この状態にあるシステムは入力の数だけ低次元化されます。）

極配置法による切換超平面の設計

次の線形時不変かつ可制御なシステムを制御対象とします。

(1) $\begin{eqnarray*} \dot{x}=Ax+Bu\\ \end{eqnarray*}$

ここで、 $x\in R^n, u\in R^m$ , Sは切換超平面で、Bは次の $B_1, B_2$ で構成されているとします。

(2) $\begin{eqnarray*} B=\begin{bmatrix} B_1 \\ B_2 \\ \end{bmatrix} , {\rm det}B_2\neq0 \end{eqnarray*}$

この時、次の変換行列 T を定義します。

(3) $\begin{eqnarray*} T= \left[\begin{array}{c} I_n-m & -B_1B_2^{-1} \\ 0 & I_m\\ \end{array}\right] , {\rm det}T\neq0 \end{eqnarray*}$

システム (1) をつぎの座標変換で正準系に変換します。

(4) $\begin{eqnarray*} x=T^{-1} \begin{bmatrix} z_1 \\ z_2 \end{bmatrix}, x_1\in R^{n-m}, x_2\in R^m \end{eqnarray*}$

上式より、システム (1) は

(5) $\begin{eqnarray*} \begin{bmatrix} \dot{z_1} \\ \dot{z_2} \end{bmatrix}= TAT^{-1}+TBu=\tilde{A}x+\tilde{B}u \\ = \begin{bmatrix} \tilde{A_{11}} & \tilde{A_{12}} \\ \tilde{A_{21}} & \tilde{A_{22} } \end{bmatrix} \begin{bmatrix} z_1 \ z_2 \ \end{bmatrix} + \begin{bmatrix} 0 \\ B_2 \\ \end{bmatrix} u \end{eqnarray*}$

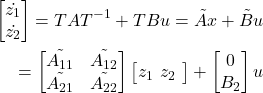
となります。正準系に変換されたシステム(5)に対してスライディングモード制御系を構成するためにつぎの切換関数を定義します。

(6) $\begin{eqnarray*} \sigma =Sz= [S_1 \hspace{10px} S_2] \begin{bmatrix} z_1 \\ z_2 \\ \end{bmatrix} \end{eqnarray*}$

スライディングモード中のときは $\sigma=0$ となるので、 $z_2=-S_2^{-1}S_1z_1$ となり $z_2$ が $z_1$ のサブシステムへの入力となります。
よって、等価制御系はつぎのようになります。

(7) $\begin{eqnarray*} \dot{z_1}=(\tilde{A_{11}}-\tilde{A_{12}}S_2^{-1}S_1)z_1 \end{eqnarray*}$

ここで、行列 $F=S^{-1}_2S_1$ とおけば

(8) $\begin{eqnarray*} \dot{z_1}=(\tilde{A_{11}}-\tilde{A_{12}}F)z_1 \end{eqnarray*}$

となり、現代制御理論で用いられる状態フィードバック系 $\dot{x}=(A-BF)x$ と同じ形となります。
よって、等価制御系の任意の極配置が可能となります。切換超平面 $S$ は

(9) $\begin{eqnarray*} S=[S_1\hspace{10px}S_2]=[S_2F\hspace{10px}S_2]=S_2[F\hspace{10px}I_m] \end{eqnarray*}$

となります。 $S_2$ は任意の正則行列なので、 $S_2=I_m$ とおけば

(10) $\begin{eqnarray*} S=[F\hspace{10px}I_m] \end{eqnarray*}$

となり行列Fにより、座標変換後の切換超平面S が決定されることがわかります。

切換超平面の設計例(極配置法)

設計例1

今回は以下のような1自由度振動系に対して切換超平面を設計します。

1自由度振動系の状態方程式はつぎのように表すことができます。ただし $m=1, k=1, d=1$ とし、状態変数は $x1=x, x2=\dot{x}$ とする。

(11) $\begin{eqnarray*} \begin{bmatrix} \dot{x_1} \\ \dot{x_2} \end{bmatrix}=\begin{bmatrix} 0 & 1 \\ -\frac{k}{m} & -\frac{d}{m} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \end{bmatrix} u \end{eqnarray*}$

この状態方程式は既に正準系の形をしているので、座標変換は行いません。
（座標変換しても式は変化しません）
よって、 $A_{11}=0, A_{12}=1$ なので等価制御系は

(12) $\begin{eqnarray*} \dot{x}=(0-F)x\\ \end{eqnarray*}$

となります。
ここで、等価制御系の極の個数は1なので（1入力2次系より）、その極を負に配置するようなFを求めてやれば状態を原点に漸近させる切換超平面は求まります。
よって今回は-5に極を配置することを考えれば、F=5となるので求めたい超平面は

(13) $\begin{eqnarray*} S=[5\hspace{10px}1] \end{eqnarray*}$

となります。

Scilab

// サブシステムの行列
A11 = [1];
A12 = [1];
S2 = eye(1);

// 配置したい極を指定
p = [-5];

// 超平面の設計
F = ppol(A11,A12,p)
S = S2*[F S2]

//切換超平面Sの値をコンソールに出力
disp("切換超平面：S=")
disp(S)

【制御理論入門】古典・現代制御の基本原理
 【Python】制御工学シミュレーション