最短経路探索などでよく使われている「A*アルゴリズム」について紹介します。
A*(A-star)経路探索とは
A-starアルゴリズムは、Peter E, Hartらによって提案された経路探索アルゴリズムです。
各頂点nからゴールまでの距離の推定値![]() を知っていた場合に対して最短経路問題を効率的に解くことができます。
を知っていた場合に対して最短経路問題を効率的に解くことができます。
このアルゴリズムでは、スタートノードからあるノードnを通ってゴールノードまでたどり着くときの最短経路を考えます。
A*アルゴリズムの処理手順
A-starアルゴリズムの大まかな処理の流れは以下の通りです。
① スタートノードS、ゴールノードG、Openリスト、Closeリストを用意する。
② SをOpenリストに追加する。
・Sの推定コスト![]() を以下の計算式で求める。
を以下の計算式で求める。
(1) ![]()
③ Openリストが空なら探索失敗として終了する。そうでなければ、Openリストから最小の![]() を持つノードを抽出し、これを親ノードnとする。
を持つノードを抽出し、これを親ノードnとする。
・親ノードnがゴールノードGと同じ(n=G)なら探索処理を終了して手順⑥へ進む。そうでなければ親ノードnをOpenリストから削除してCloseリストに追加する。
・親ノードnに隣接する移動可能な全てのノードを子ノードmとする。
④ 全ての子ノードmの仮推定コスト![]() を以下の計算式から求める。
を以下の計算式から求める。
(2) ![]()
・状態と仮推定コスト![]() の値に応じて、各子ノードmに対して(a)~(d)のいずれかの操作を行う。
の値に応じて、各子ノードmに対して(a)~(d)のいずれかの操作を行う。
(a)「子ノードm状態がNone」の場合
・![]() とする。
とする。
・子ノードmをOpenリストに追加する。
・子ノードmの親をnとして記録する。
(b)「子ノードm状態がOpen」かつ「![]() 」の場合
」の場合
・![]() に置き換える。
に置き換える。
・子ノードmの親をnとして記録する。
(c)「子ノードm状態がClose」かつ「![]() 」の場合
」の場合
・![]() なら
なら![]() に置き換える。
に置き換える。
・子ノードmをCloseリストから削除してOpenリストに追加する。
・子ノードmの親をnとして記録する。
(d)上記以外の場合は何もしない。
⑤ ③以降を繰り返す。
⑥ 探索終了後、ゴールノードGから記録しておいた親ノードnを順次辿ると最短経路が得られる。
ノードn:親ノード
ノードm:子ノード(親ノードnに隣接している移動可能なノード)
![]() :親ノードnからゴールノードまでの推定最小コスト(最短距離)
:親ノードnからゴールノードまでの推定最小コスト(最短距離)
![]() :スタートノードから親ノードnまでの推定最小コスト(最短距離)
:スタートノードから親ノードnまでの推定最小コスト(最短距離)
![]() :親ノードnから子ノードmへ移動するときのコスト(距離)
:親ノードnから子ノードmへ移動するときのコスト(距離)
![]() :スタートノードから子ノードmを経由してゴールノードに到達するまでの推定最小コスト(最短距離)
:スタートノードから子ノードmを経由してゴールノードに到達するまでの推定最小コスト(最短距離)
![]() :
:![]() の候補値で
の候補値で![]() で算出
で算出
ステータス:ノードの状態(初期状態:None、計算中:Open、計算済:Close)
Openリスト:状態がOpen(計算中)のノードを格納するリスト
Closeリスト:状態がClose(計算済み)のノードを格納するリスト
A-starアルゴリズムの計算例
今回の計算例では、各推定値を以下の値で計算します。
![]() :子ノードnからゴールノードGまでのマンハッタン距離
:子ノードnからゴールノードGまでのマンハッタン距離
![]() :スタートノードSから親ノードnまでのマンハッタン距離
:スタートノードSから親ノードnまでのマンハッタン距離
![]() :1
:1
![]() :
:![]()
![]() :子ノードmが複数ある場合、それぞれの
:子ノードmが複数ある場合、それぞれの![]() の中で最も小さい値
の中で最も小さい値
(子ノードmが1の場合は![]() )
)
1.スタートノード、 ゴールノード、Openリスト、Closeリストを用意
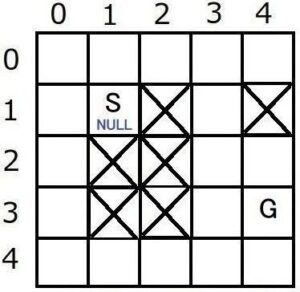
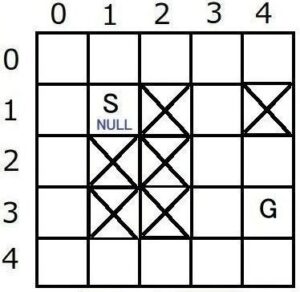
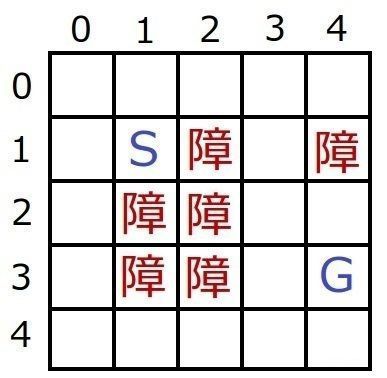
今回の数値例では、以下のような縦横5マスの地図を対象としてS~Gの最短経路を求めます。
(斜め移動は可能:8方向移動、障:障害物で移動不可)
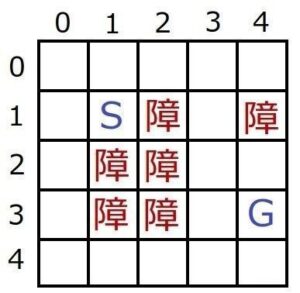
元地図から各ノードの「状態と推定コストを記録するマップ」と「親ノードの位置を記録するマップ」を用意します。
「状態と推定コストを記録するマップ」がスタートノードS、 ゴールノードG、Openリスト、Closeリストに相当します。
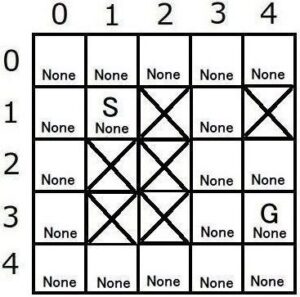
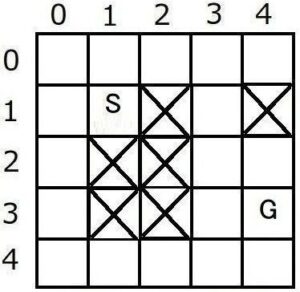
2. スタートノードのOpenリスト追加と推定コスト計算
スタートノードSの状態をNoneからOpenにします。(Openリストに追加)
スタートノードSの親ノードの位置を記録します。(Sに親ノードはないのでNull)
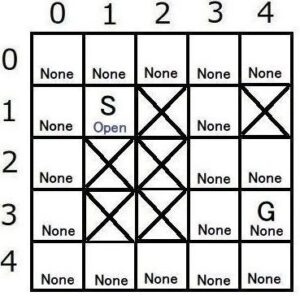
![]() を計算します。(Sは1つしかないので
を計算します。(Sは1つしかないので![]() となる)
となる)
(3) ![]()
![]() はスタート地点なので0となります。
はスタート地点なので0となります。
![]() は障害物は無視したスタートノード(S)とゴールノード(G)のマンハッタン距離なので5となります。
は障害物は無視したスタートノード(S)とゴールノード(G)のマンハッタン距離なので5となります。
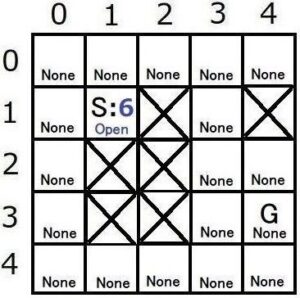
よって、![]() は6になります。(Sの推定コスト6をマップに記録)
は6になります。(Sの推定コスト6をマップに記録)
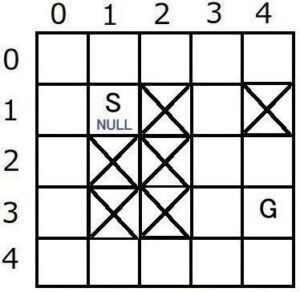
##3. 親ノードと子ノードの決定
マップにはOpen状態のノード(スタートノードS)があります。(=Openリストは空でない)
よって、探索は続行します。
Open状態のノードはスタートノードSしかないため、これを親ノードnに設定します。
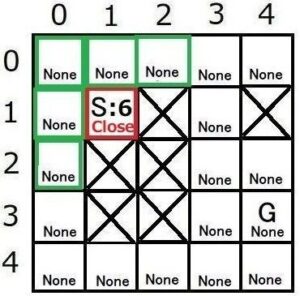
![]() なので、探索終了せず親ノードSの状態をCloseにします。(Closeリストに追加)
なので、探索終了せず親ノードSの状態をCloseにします。(Closeリストに追加)
親ノードSに隣接する移動可能な全てのノードを子ノードmに選びます。
4. 子ノードの探索
全ての子ノードmの仮推定コスト![]() を計算します。(mは5つあるので
を計算します。(mは5つあるので![]() も5つ計算)
も5つ計算)
(4) ![]()
上式より子ノードmからゴールノードまでのマンハッタン距離を計算すれば![]() が求まります。
が求まります。
(例:子ノード![]() の場合、m~Gのマンハッタン距離は7なので推定コストは9となります。
の場合、m~Gのマンハッタン距離は7なので推定コストは9となります。
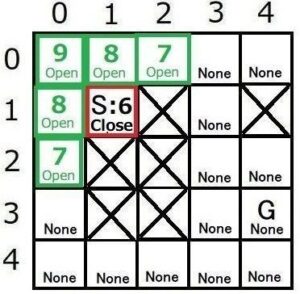
5つの子ノードmの状態はNoneなので、![]() とし ます。(
とし ます。(![]() の値はマップに記録)
の値はマップに記録)
また、5つの子ノードmの状態をOpenにします。(Openリストに追加)
5つの子ノードmの親ノードSをマップに記録します。
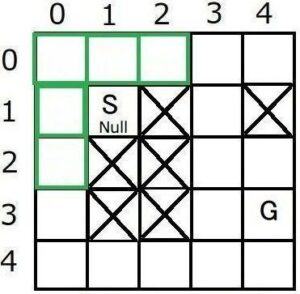
3. 次の親ノードと子ノードの決定
マップにはOpen状態のノードが5つあります。(=Openリストは空でない)
よって、探索は続行します。
状態がOpenで推定コスト![]() が最小なノードを次の親ノードnに設定します。
が最小なノードを次の親ノードnに設定します。
親ノードの条件を満たすノードは![]() の2つあります。
の2つあります。
どちらを選んでもいいですが、今回はノード![]() を親ノードにして計算します。
を親ノードにして計算します。
親ノード![]() はGと同じではないので、探索は終了せず親ノード
はGと同じではないので、探索は終了せず親ノード![]() の状態をCloseにします。(Closeリストに追加)
の状態をCloseにします。(Closeリストに追加)
親ノード![]() に隣接する障害物以外のノードを子ノードに選びます。
に隣接する障害物以外のノードを子ノードに選びます。

4. 次の子ノードを探索
![]() を計算します。(子ノードmは3つあるので
を計算します。(子ノードmは3つあるので![]() を3つ計算する)
を3つ計算する)
(5) ![]()
よって、2つの子ノードmからゴールノードまでのマンハッタン距離を計算すれば![]() も求まります。
も求まります。
(例:子ノード![]() ~ゴールノードGのマンハッタン距離は6なのでこのノードの推定コスト
~ゴールノードGのマンハッタン距離は6なのでこのノードの推定コスト![]() は9(=6+3)となります。
は9(=6+3)となります。
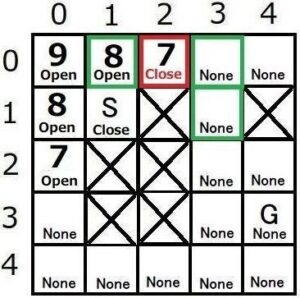
3つの子ノードmのうち、![]() の状態はNoneなので、
の状態はNoneなので、![]() とします。(
とします。(![]() の値はマップに記録)
の値はマップに記録)
![]() の状態をOpenにします。(Openリストに追加)
の状態をOpenにします。(Openリストに追加)
![]() の親ノードSをマップに記録します。
の親ノードSをマップに記録します。
残り1つの子ノード![]() の状態はOpenで仮推定コスト
の状態はOpenで仮推定コスト![]() は9です。
は9です。
前回の計算結果より![]() は8なので
は8なので![]() となります。
となります。
よって![]() に関しては何も操作を行いません。
に関しては何も操作を行いません。
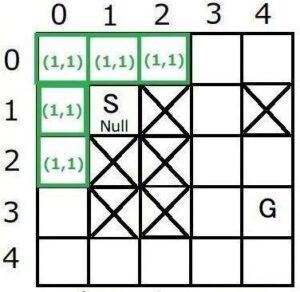
5. 探索の繰り返し
以後、「3.次の親ノードnと子ノードnを決定」→「 次の子ノードmを探索」を繰り返していきます。
すると、何回か繰り返すうちに親ノードnがゴールノードmに到達します。(探索終了)
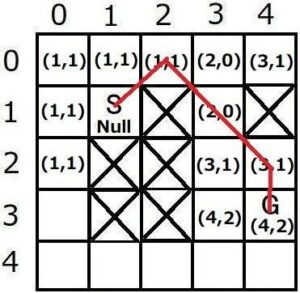
その時のマップは以下のようになります。
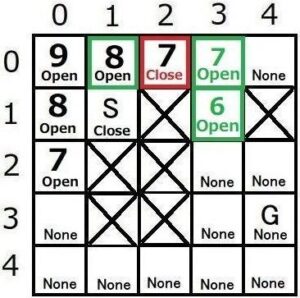
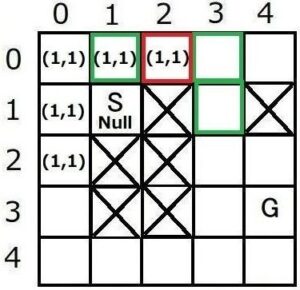
6. 親ノードを辿って経路を求める
親ノードを記録したマップを用いて、ゴールノードGから親ノードnを辿っていきます。
(ゴールノード![]() の親ノードは
の親ノードは![]() 、
、![]() の親ノードは
の親ノードは![]() ・・・)
・・・)
すると、最終的にスタートノードSまでたどりつきます。これが最短経路の各座標となります。
(4,3)→(4,2)→(3,1)→(2,0)→(1,1)
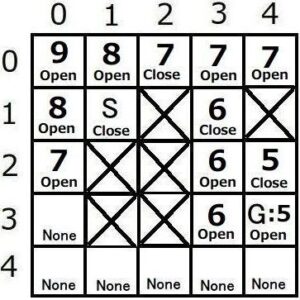
以上で、A*アルゴリズムの説明は終わりとなります。

コメント