この記事では、QR法で行列の固有値を計算する方法ついて解説します。
QR分解とは
QR分解とは、線形代数において行列を直交行列Qと、上三角行列Rの積に分解する手法です。
(1) ![]()
QR法による固有値の計算
n次元の行列Aを定義します。
そして、
(2) ![]()
とおきます。そして、
(3) 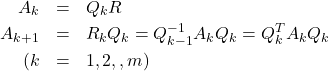
とQR分解と対角化(![]() )を繰り返していきます。
)を繰り返していきます。
このとき、このとき、![]() の固有値はすべて一致します。
の固有値はすべて一致します。
つまりこれを何度も繰り返すことで、対角化すればその対角成分を調べる事で行列Aの固有値を知ることができます。
【関連記事】線形代数入門



コメント