画像処理における1次微分フィルタの原理や特徴、計算式についてまとめました。
一次微分フィルタとは
一次微分フィルタは、画像処理において輪郭検出に使用されるフィルタです。
一次微分を計算することで、注目画素の左右・上下の画素値の変化の傾きが求まります。
画像の輪郭は画素値の変化が大きいため、微分した画素値が大きい箇所が輪郭となります。
■入力画像(左)、出力画像(右)


出力画像を見ると、輪郭の部分が白くなっています。
出力画像の白い部分は、画素値が大きい、つまり一次微分を計算したときに画素値の変化が大きいところとなります。
(例:背景とヘルメットの境界など)
一次微分フィルタのカーネル
注目画素$I(x, y)$と周囲の画素値について考えます。
$$ I=\begin{bmatrix}I(x-1, y-1) & I(x, y-1) & I(x+1, y-1) \\ I(x-1, y) & I(x, y) & I(x+1, y) \\ I(x-1, y+1) & I(x, y+1) & I(x+1, y+1)\end{bmatrix} \quad $$
画像データの微分は差分で計算することができます。よって、注目画素$I(x, y)$の水平方向、および垂直方向それぞれの一次微分$I_{x}(x, y), I_{y}(x, y)$は次のようになります。
$$ I_{x}(x, y)=I(x+1,y)-I(x, y) \\ I_{y}(x, y)=I(x, y+1)-I(x, y) $$
よって、一次微分フィルタの水平方向微分のカーネル$K_x$、および垂直方向微分に用いるカーネル$K_y$は次のようになります。
$$ K_x=\begin{bmatrix} 0 & 0 & 0 \\ 0 & -1 & 1 \\ 0 & 0 & 0 \end{bmatrix} \quad ,K_y=\begin{bmatrix} 0 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 1 & 0\end{bmatrix} \quad $$
ただし、このやり方だと、実際には2つの画素の中間における微分値($I_{x}(x+0.5, y), I_{y}(x, y+0.5)$)となってしまいます。そこで、注目画素の両端の画素値の差分を計算することで、注目画素の位置に合わせる方法もあります。
$$ I_{x}(x, y) = I(x+1,y)-I(x-1, y) \\ I_{y}(x, y) = I(x, y+1)-I(x, y-1) $$
このとき、水平方向微分のカーネル$K_x$、および垂直方向微分に用いるカーネル$K_y$は次のようになります。
$$ K_x=\begin{bmatrix} 0 & 0 & 0 \\ -1 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix} \quad ,K_y=\begin{bmatrix} 0 & -1 & 0 \\ 0 & 0 & 0 \\ 0 & 1 & 0\end{bmatrix} \quad $$
水平方向微分では縦方向の輪郭を取り出すことができます。逆に、垂直方向微分では横方向の輪郭を取り出します。入力画像$I$とカーネル$K_x$および$K_y$を使用して、輪郭検出を行います。垂直方向および水平方向の輪郭画像$I_x(x, y)$および$I_y(x, y)$は次のように計算されます。
$$I_x(x, y) = I(x, y) \ast K_x\\ I_y(x, y) = I(x, y) \ast K_y$$
ここで、$\ast$は畳み込み演算を示します。
最後に、縦方向に検出された輪郭画像の画素値を$I_{x}(x, y)$、横方向に検出された輪郭画像の画素値を$I_{y}(x, y)$とすると、縦横両方向の輪郭画像の画素値$I'(x, y)$は、次式で計算できます(二乗和平方根)。
$$ I'(x, y) = \sqrt{I_{x}(x, y)^2 + I_{y}(x, y)^2} $$
一次微分フィルタの計算例
次のような入力画像$I$と一次微分フィルタ(垂直方向微分)のカーネル$K_y$が与えられたとき、出力画像$I’$を求めます。
$$ I=\begin{bmatrix}0 & 0 & 0 & 0 \\ 0 & 10 & 10 & 0 \\ 0 & 0 & 10 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}, K=\begin{bmatrix} 0 & -1 & 0 \\ 0 & 0 & 0 \\ 0 & 1 & 0\end{bmatrix} \quad $$
入力画像$I$とカーネル$K_y$を畳み込み演算してやると、$ I'(1,1)=0$、 $I'(2,1)=(1\cdot 10)=10$、 $I'(1,2)=(-1\cdot 10)=-10$、 $I'(2,2)=(-1\cdot 10)=-10 $となります。端の画素値は0とすれば出力画像$I’$は次のようになります。
$$ I’=\begin{bmatrix}0 & 0 & 0 & 0 \\ 0 & 0 & 10 & 0 \\ 0 & -10 & -10 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \quad $$
また、負の値となっている画素値を絶対値を取って正の値にすると、出力画像$I’$は次のようになります。
$$ I’=\begin{bmatrix}0 & 0 & 0 & 0 \\ 0 & 0 & 10 & 0 \\ 0 & 10 & 10 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \quad $$
負の値となっている画素値を0にした場合、出力画像$I’$は次のようになります。
$$ I’=\begin{bmatrix}0 & 0 & 0 & 0 \\ 0 & 0 & 10 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \quad $$
このように、負の値をどのように扱うかで出力結果は異なるため、プログラミングで実装する際には注意が必要です。
関連ページ
プログラミングによる実装例について下記事で解説しています。



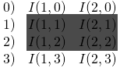

コメント
Ix,Iyからカーネルになる過程がわかりません
よかったら教えてください