【画像処理】HSV色空間の原理・特徴・計算式

HSV色空間の原理や特徴、計算式についてまとめました。

HSV色空間とは
【換算式】RGB色空間からHSV色空間への変換
関連ページ

HSV色空間とは

HSV色空間とは、「色相(Hue)」「彩度(Saturation)」「明度(Value)」の3つの組み合わせで色を表現する手法です。

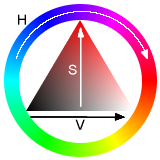
–	説明
色相(H)	色合い。（赤っぽい、青っぽいといった色のおおまかな違いのことで、赤なら0度、黄色なら 60度といったように角度で色合いが決まります）
彩度(S)	色の鮮やかさ。（色相が同じ場合でも、彩度が高ければ鮮やかに見え、低ければグレーに見える。彩度がゼロの場合は無彩色[黒、グレー、白]）
明度(V)	色の明るさ。（高いほど明るい色になる）

HSV色空間は人間が色を知覚する方法と類似しているため、RGB色空間よりも人がイメージした通りの色を作りやすいという特徴があります。
この特徴から、画像処理でも色検出をおこなう場合などにHSV色空間が利用されています。

【換算式】RGB色空間からHSV色空間への変換

（R、G、B）の値が0.0(最小)から1.0（最大）の範囲にあるとします。
R,G,Bの3つの値のうち、最大のものをMAX、最小のものをMINとしたとき、色相(H)は以下の式で計算できます。

(1) $\begin{eqnarray*} H= \left{ \begin{array}{r@{\,}c@{\,}r@{\,}c@{\,}r@{\;\leq\;}r} undefined \hspace{10px}(MIN=MAX)\\ 60\times \frac{G-R}{MAX-MIN}+60\hspace{10px}(MAX=B)\\ 60\times \frac{B-G}{MAX-MIN}+120\hspace{10px}(MAX=R)\\ 60\times \frac{R-B}{MAX-MIN}+240\hspace{10px}(MAX=G)\\ \end{array}% \right. \end{eqnarray*}$