ヒストグラム平均化(平坦化)による写真鮮明化の原理や計算式についてまとめました。
ヒストグラム平均化とは
本ページの内容は以下動画で解説しています。
画像のヒストグラムの形から、画像の状態(全体的に暗すぎるか、逆に明るすぎるか等)を知ることができます。
| ヒストグラムの形 | 画像の状態 |
|---|---|
| 山が左寄り | 暗い画像 |
| 山が右寄り | 明るい画像 |
| 山が中央寄り | コントラストが低い |
なお、「ヒストグラムと何か?」という話は以下ページで紹介しています。

画像データのヒストグラムとは?形状や山の見方を解説
写真等の画像データのヒストグラムとは?形状や山の見方を解説します。
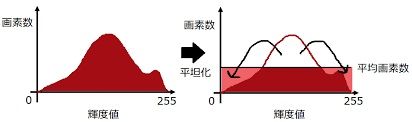
そこで、ヒストグラムが全体的に平均化されるよう画像の画素値を変換してやると、人が見やすい画像なります。
これをヒストグラム平均化(平坦化)といいます。
平均画素数=全画素数/階調数=(画像の幅×高さ )/256
例)画像サイズが256*256の場合は、平均画素数は256
例)画像サイズが256*256の場合は、平均画素数は256
全ての画素値(0~255)の度数が平均画素数になるように変換するのが、理想的なヒストグラム平均化です。
ただし実際の処理では、画素数が多い範囲で、画素値の間隔を粗くします。
逆に画素数が少ない範囲では、画素値の間隔を細かくします。
計算式
全ての画素値(0~255)の度数が平均画素数になるように変換するのが、理想的なヒストグラム平均化です。
座標![]() における入力画像の画素値を
における入力画像の画素値を![]() 、その度数を
、その度数を![]() とします。
とします。
また、入力画像の画素値の最大値を![]() 、入力画像の総画素数を
、入力画像の総画素数を![]() とします。
とします。
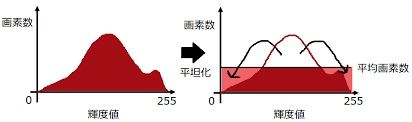
このとき、理想的なヒストグラム平均化を行った出力画像の画素値![]() は以下の式で計算できます。
は以下の式で計算できます。
(1) 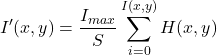
プログラミングによる実装
プログラミングによる実装例については以下ページで解説しています。

【Python/OpenCV】cv2.equalizeHistで画像のヒストグラムを平均化して見やすい画像に変換
Python版OpenCVの「cv2.equalizeHist」で画像のヒストグラムを平均化して見やすい画像に変換する方法をソースコード付きで解説します。
関連ページ

【画像処理超入門】アルゴリズムの仕組みと実装方法を簡単に解説
画像処理超アルゴリズムの仕組みとプログラミングによる実装方法を簡単に解説します。


コメント
H(x,y)->Hi
では?