この記事では、ロール・ピッチ・ヨー角による姿勢表現について紹介します。
ロール・ピッチ・ヨー角による姿勢表現
乗り物やロボットなどの姿勢は、オイラー角と呼ばれる3つの回転軸を使って表現されます。
この3つの回転軸は、ロボットでは![]() (軸の取り方は色々)、物理学では
(軸の取り方は色々)、物理学では![]() ,乗り物ではロール・ピッチ・ヨーで表されますが、これらは基本的に同じです。
,乗り物ではロール・ピッチ・ヨーで表されますが、これらは基本的に同じです。
ロール角(γ)・・・x軸(物体の前後)を回転軸とする回転角 ピッチ角(β)・・・y軸(物体の左右)を回転軸とする回転角 ヨー角(α)・・・z軸(物体の上下)を回転軸とする回転角
ロール・ピッチ・ヨーを飛行機で表すと以下のようになります。

※1. 対象とする物体は、乗り物など前後・左右・上下が決まった物である必要があります。
※2. 回転の向きは右ねじが軸方向に進むときに右ねじが回る向きです。
αγβの姿勢変換行列
3つの座標軸![]() まわりに順に
まわりに順に![]() 回転させることにより姿勢の変換を表現します。
回転させることにより姿勢の変換を表現します。
このとき、![]() の変換行列
の変換行列![]() はつぎのようになります。
はつぎのようになります。
(1) 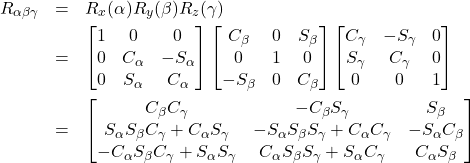
この式を使えば、3つの回転角から変換行列を求めることが出来ます。
ただし、
(2) 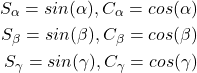
です。
| – | 関連ページ |
|---|---|
| 1 | ■Pythonでロボットシミュレーション |
| 2 | ■ロボット工学入門 基礎編 |
| 3 | ■Python入門 サンプル集 |
| 4 | ■NumPy入門 サンプル集 |

コメント