【強化学習】マルコフ決定過程（MDP）の原理・例題・計算方法

強化学習などで使われるマルコフ決定過程（MDP）の原理・アルゴリズムについて入門者向けにまとめました。

マルコフ決定過程（MDP）とは

マルコフ決定過程(Markov decision process: MDP)とは、次に起こる事象の確率が、これまでの過程と関係なく、現在の状態によってのみ決定される確率過程のことです。
このような、以前の状態に依存しない性質のことを「マルコフ性」といいます。

マルコフ過程の例題

例えば、天気の状態遷移が以下のマルコフ過程に従うとします。

今日＼明日 晴れ 曇り 雨
晴れ 40 40 20
曇り 30 40 30
雨 30 50 20

単位：％

このマルコフ過程では、「晴れの翌日の天気は、40%の確率で晴れ、40%の確率で曇り、20%の確率で雨である」ことを表しています。
つまり、前日までの天気状態によらず明日の天気の確率が決まります。

例題

問）天気が雨の日の2日後が晴れである確率は何％か。
天気の移り変わりが単純マルコフ過程であると考えたとき，雨の2日後が晴れである確率は何%か。

回答）
天気が雨の日の2日後が晴れになるのは、次の3通りの場合があります。

今日 明日 2日後 確率
雨 晴れ 晴れ 0.3×0.4＝0.12
雨 曇り 晴れ 0.5×0.3＝0.15
雨 雨 晴れ 0.2×0.3＝0.06

それぞれの確率を足し合わせると、0.33となります。
よって、答えは33%となります。
※この問題は基本情報技術者試験で出題されたものです。

強化学習におけるマルコフ決定過程モデル

強化学習では、マルコフ決定過程モデルを集合の数式を使って次のように表現します。
時刻tにおいて環境状態がsのとき、エージェントは行動aを選択して実行します。
すると、次の時刻t+1において環境は確率的に状態s'へ遷移します。
強化学習では、利益(=累積報酬)を最大化する行動選択の規則\pi(=政策)を学習します。

(1)   \begin{eqnarray*} s \in S = \{ s_1 ,s_2 , \cdots ,s_n \} \\ a \in A = \{ a_1 , a_2 , \cdots , a_n \} \\ P(s' | s,a) \\ R(s, a, s') \\ \pi(s, a) \end{eqnarray*}

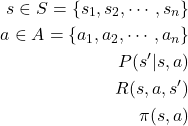
記号 説明 先程の例題
s 時刻tにおける環境の状態 今日の天気
a 時刻tにおけるエージェントの行動 明日の天気
S 環境がとる有限な状態集合 晴れ、曇り、雨
A エージェントがとる有限な行動集合 晴れ、曇り、雨
P(s' | s,a) 【遷移関数】次の環境状態s'へ遷移する確率
R(s, a, s') 【評価関数】次の環境状態s'からエージェントへ与えられる報酬rの期待値(報酬は確率的に与えられ、その条件付き期待値)
\pi(s, a) 政策\piのもとである環境状態sにおいて行動aを選択する確率
– 関連ページ・参考文献
関連記事 ■【機械学習入門】アルゴリズム＆プログラミング
参考文献 ■強化学習 ■強化学習の基礎 ■強化学習の基礎 ■強化学習について学んでみた。 ■情報意味論(12)強化学習 ■Emergent Computation ■Q学習による最短経路学習 ■Pythonではじめる強化学習 ■強化学習入門 ～これから強化学習を学びたい人のための基礎知識～

コメント