機械学習のアルゴリズム(原理)やプログラミング方法について入門者向けにまとめました。
【機械学習とは】教師あり、教師なし学習の違い
機械学習(machine learning)とは、人間が経験的に行っている様々な学習活動を、コンピュータでも実現させるための技術です。
コンピュータの発展とともに機械学習の技術も飛躍的に向上しています。
様々な分野に応用されていますが一例を挙げると以下の通りです。
| 分野 | 機械学習の実用例 |
|---|---|
| 金融 | 過去のデータから株価予測 |
| 医療 | 過去の患者達のデータから病気を判別 |
| 自動車 | 自動運転 |
機械学習の基本用語はつぎのとおりです。
| – | 機械学習の基本用語 |
|---|---|
| 学習 | 大量のデータ(説明変数・目的変数)から最適なパラメータ(予測を計算するための係数、重みなど)を計算すること。 |
| モデル | 利用するモデル式、計算したパラメータ群 |
| 予測 | モデルに入力(新しい説明変数)を与えて出力(目的変数)を計算すること。 |
「問題の性質」「学習時間」「手持ちのデータの量・質」「実装・運用時のコスト」「解釈の容易性(結果説明のしやすさ)」「予測精度(性能)」を考慮して最適な学習方法を選択します。
(※一般的に「解釈の容易性」と「予測精度」はトレードオフの関係にあります)
教師あり・なし学習
機械学習の手法は様々ですが、大別すると以下の3つあります。
| 種別 | 概要 |
|---|---|
| 教師あり学習 | 教師データを用いて学習を行う。さらに教師あり学習は「回帰」と「分類」に大別される。回帰は、入力データ(説明変数)に対応する出力値(目的変数)を近似(予測)する。分類は入力がどのクラスに属するかを判別する。 |
| 教師なし学習 | 教師データを用いずに学習を行う。代表的な手法は「クラスタリング」と「次元削減」。 |
| 強化学習 | 収益を最大化するような方策を獲得する。 |
【教師あり学習(回帰)】線形回帰(単回帰・重回帰)
回帰分析では、「結果データ」と「結果に影響を及ぼすデータ」の関係性を統計的に求める手法です。この2つのデータの関係性がわかれば、将来どのような結果となるかの予測を行うことができます。このとき、結果データを「目的変数」、結果に影響を及ぼすデータを「説明変数」といいます。
(一般化)線形回帰は、連続値を予測します。
説明変数が1つの場合は「単回帰」、複数の場合は「重回帰」といいます。
| – | 線形回帰の詳細 |
|---|---|
| 特性 | 予測対象:連続値, 学習タイプ:教師あり, 可読性:○, 並列処理:✕ |
| 特徴 | ・最小二乗法や最尤推定によって回帰直線の係数と切片を求めます。 ・重回帰分析を行う場合、多重共線性(相関係数が高い特徴量の組を同時に説明変数に選択すると、予測精度が悪くなる現象)に注意する必要がある。具体的には、相関係数(特徴量同士の相関の正負の強さを-1以上1以下の値で表す)が±1に近い特徴量の組を作らないように、各組の相関係数を見ながら特徴量をうまく取り除く。 |
| 原理 | 単回帰分析、重回帰分析、多重共線性 |
| 実装 | Python(単回帰分析・Scikit-learn)、Python(重回帰分析・Scikit-learn) |
【教師あり学習(分類)】ロジスティック回帰、サポートベクタマシン、決定木、ランダムフォレスト、knn法、ニューラルネットワーク
ロジスティック回帰
| – | 概要 |
|---|---|
| 特性 | 予測対象:分類, 学習タイプ:教師あり, 可読性:○, 並列処理:✕ |
| 特徴 | ・2分類問題に対応(線形回帰の出力をロジット関数に入力) ・回帰による分類法 ・対数オッズと呼ばれる値を重回帰分析で予測し、対数オッズにロジット変換(出力値が正規化される)を行うことで、クラスiに属する確率piの予測値を計算し、最大確率を実現するクラスがデータが属するクラスと判定する ・目的関数には、尤度関数が用いられる |
| 実装 | Python(Scikit-learn) |
サポートベクターマシン
| – | 概要 |
|---|---|
| 特性 | 予測対象:分類, 学習タイプ:教師あり, 可読性:○, 並列処理:✕ |
| 特徴 | ・マージン最大化という考え方を用いることで、汎化性能が高い2分類を実現 ・誤分類を許容するための工夫として「スラック変数」を利用 ・データを高次元空間に写像し、そこで線形分離:SVMし、得られた境界線を元の空間に戻す、カーネル法(カーネル関数による計算)というアイデアで、線形分離可能でないデータに対しても決定境界を求めることが可能 ・カーネル法の計算量は膨大なため、カーネルトリックという手法で計算量をうまく低減している |
| 原理 | SVM(サポートベクタマシン)の基本 |
| 実装 | Python(Scikit-learn)、Python(OpenCV) |
決定木
| – | 概要 |
|---|---|
| 特性 | モデル:木構造(非線形), 学習タイプ:教師あり, 予測対象:分類, 可読性:○, 並列処理:✕ |
| 特徴 | ・枝先で1つの説明変数と閾値のセットで、データを2つに分ける(条件分岐)のを繰り返す。 ・説明変数の選択と閾値は、ジニ不純度(ジニ係数)やエントロピー等で決定(不純度が最小=情報利得を最大化するための条件分岐) ・「データのスケールを事前にあわせる必要がない」「分析結果の説明が容易」という利点がある |
| 実装 | Python(Scikit-learn) |
ランダムフォレスト
| – | 概要 |
|---|---|
| 特性 | モデル:木構造(非線形), 学習タイプ:教師あり, 予測対象:分類, 可読性:○, 並列処理:✕ |
| 特徴 | ・決定木とバギング(アンサンブル学習の1つ)という複数のモデルを利用して、それらの平均の多数決を予測結果とする)を組み合わせた手法 ・決定木の利点を引き継ぎ、決定木の欠点であった過学習の起こしやすさを改善している ・データの前処理が少ない ・安定した良い精度が得られる ・ハイパーパラメータ:木の最大深さ、ノードのデータの最小数など |
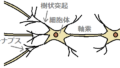
ニューラルネットワーク(多層パーセプトロン)
| – | 概要 |
|---|---|
| 特性 | モデル:神経回路, 学習タイプ:教師あり 予測対象: 連続値・分類, 可読性:✕, 並列処理:○ |
| 特徴 | ・古典的なニューラルネットワーク ・3層構造(入力・中間・出力) ・学習にはバックプロパゲーションを用いることが多い。 ・複雑なモデルを構築できる反面、過学習も多い。 |
| 原理 | ニューラルネットワークの基本、多層パーセプトロン(MLP) |
| 実装 | Python(単純パーセプトロン)、Python(Scikit-learn) |
深層学習(ディープラーニング)
| – | 概要 |
|---|---|
| 特性 | モデル:神経回路, 学習タイプ:教師あり 予測対象: 連続値・分類, 可読性:✕, 並列処理:○ |
| 特徴 | ・ディープニューラルネットワークを用いた機械学習の手法 ・①訓練データを用いて予測を行い(順伝搬)、予測値と正解ラベルの誤差を計算 ②誤差が最小となるように勾配降下法で重みを更新(逆伝搬) ①②を繰り返す ・複雑なモデルを構築できる(利点) ・ハイパーパラメータが多い(欠点) 過学習が多い(欠点) ・勾配消失問題が起こる(欠点) |
| 原理 | 深層学習の基本、畳み込みニューラルネットワーク |
| 実装 | Python(Keras)、Python(PyTorch) |
| – | knn法 |
|---|---|
| 特性 | モデル:-, 学習タイプ:教師あり, 予測対象:分類, 可読性:○, 並列処理:✕ |
| 特徴 | ・データから近い順にk個のデータをみて、それらの多数決でデータの所属するクラスを決定 ・各クラスのデータ数に偏りがある、各クラスがよく別れていない場合に精度が低下する ・単純なアルゴリズムだが、距離計算するので訓練データが多いと計算時間が高くなる |
| 詳細 | – |
| 実装 | – |
【教師なし学習】クラスタリング、次元削減
クラスタ分析(Clustering) は、特徴が類似するデータ同士をまとめて、データ構造を発見します。
クラス分類は教師あり学習(=あらかじめ設定したクラスに対して教師データを使って学習を行う)ため、クラスタ分析とは異なるものである点に注意。
| – | 階層型クラスタ分析の詳細 |
|---|---|
| 特性 | 予測対象:分類, 学習タイプ:教師なし, 可読性:○, 並列処理:✕ |
| 特徴 | ・代表例はユークリッド距離*ウォード法 ・あらかじめ定義した距離を用いてデータをグループ化 ・クラスタ数(分類数)は、計算後に変更可能 |
| 詳細 | – |
| 実装 | – |
| – | 非階層型クラスタ分析の詳細 |
|---|---|
| 特性 | 予測対象:分類, 学習タイプ:教師なし, 可読性:✕, 並列処理:○ |
| 特徴 | ・代表例はk平均法 ・クラスタ数(分類数)を事前に指定する必要がある(後から変更不可) ・階層型クラスタリングで高速化もできる ・問題点:初期値によって結果が異なる |
| 原理 | k平均法 |
| 実装 | Python(Scikit)、Python(OpenCV) |
正則化
正則化とは、過学習を防止する手法の1つです。
正則化は、複雑すぎるモデルに対して過学習を引き起こしやすいため、パラメータのノルムを大きくしすぎないようにすれば過学習を抑制できるのではというアイデアです。
代表的なものとして、ラッソ、リッジがあります。
| 種別 | 概要 |
|---|---|
| LASSO正則化 | 自動的に特徴量の選択が行われる性質をもつ |
| Ridge正則化 | パラメータのノルムを小さく抑える(特徴量選択は行わない) |
次元削減
次元削減とは、できるだけデータの情報を失わずに、データの次元数を減らすことです。
機械学習では「構造抽出」「汎化能力の向上」「可視化」「メモリ節約」などに活用されます。
代表例として主成分分析(PCA)があります・
| – | 主成分分析(PCA)の詳細 |
|---|---|
| 特性 | 線形の次元削減を行う手法 |
| 特徴 | ・寄与率を計算することで、各成分の重要度がわかる ・主成分を計算することで、各成分の意味を推測できる |
| 詳細 | 主成分分析(PCA)の原理 |
| 実装 | ー |
| – | トピックモデルの詳細 |
|---|---|
| 特性 | 予測対象:分類, 学習タイプ:教師なし, 可読性:✕, 並列処理:○ |
| 特徴 | ・代表例はLDA ・トピック数(分類数)は事前に与える必要あり ・トピック毎の出現頻度からスコアを計算してデータを分類 ・計算量が大きい |
| 詳細 | ー |
| 実装 | ー |
【強化学習】Q-Learning、Deep Q-Learning
強化学習(Reinforcement learning)とは、エージェントがある環境内で現在の状態を観測し、収益を最大化するための取るべき行動を決定する学習手法の1つです。
つまり、エージェントが試行錯誤を繰り返していき、徐々に環境に適応した行動を取るような学習を行います。
| – | 強化学習の詳細 |
|---|---|
| 特性 | 学習タイプ:強化学習 |
| 特徴 | ・試行錯誤を繰り返し「評価値(報酬)が最大となる行動」を学習 |
| 詳細 | 強化学習の原理 |
| 実装 | ー |
【統計処理】記述統計、数理統計
統計学とは、得られたデータから、法則性や知見を数学的に得る分野です。
統計学は、次の2つに大別されます。
| – | – |
|---|---|
| 記述統計 | 標本(取得したデータそのもの)の分析を行う。例えば、学校全生徒のテスト結果を収集し、その平均点を求めるのは記述統計です。 |
| 推計統計 | 母集団(取得したデータの背後にあるデータ群)の性質を予測する。例えば、1000世帯の視聴率を調査し、そのデータから日本の全世帯を視聴率を予測するのは推計統計です。 |
【時系列データ】異常検知、類似度
| – | 詳細 |
|---|---|
| 異常検知 | ●K近傍法 ●特異スペクトル変換法 |
| 類似度 | ●コサイン類似度 ●DTW(動的時間伸縮法) |
【その他】プログラミング、便利ツール、活用事例、参考文献
プログラミング言語やライブラリ別に機械学習の実装方法を個別記事に整理しました。





コメント