単回帰分析とは?計算式の仕組みや求め方、決定係数による性能検証方法などをVTuberの視聴者数予測を例をわかりやすく解説します。
単回帰分析とは
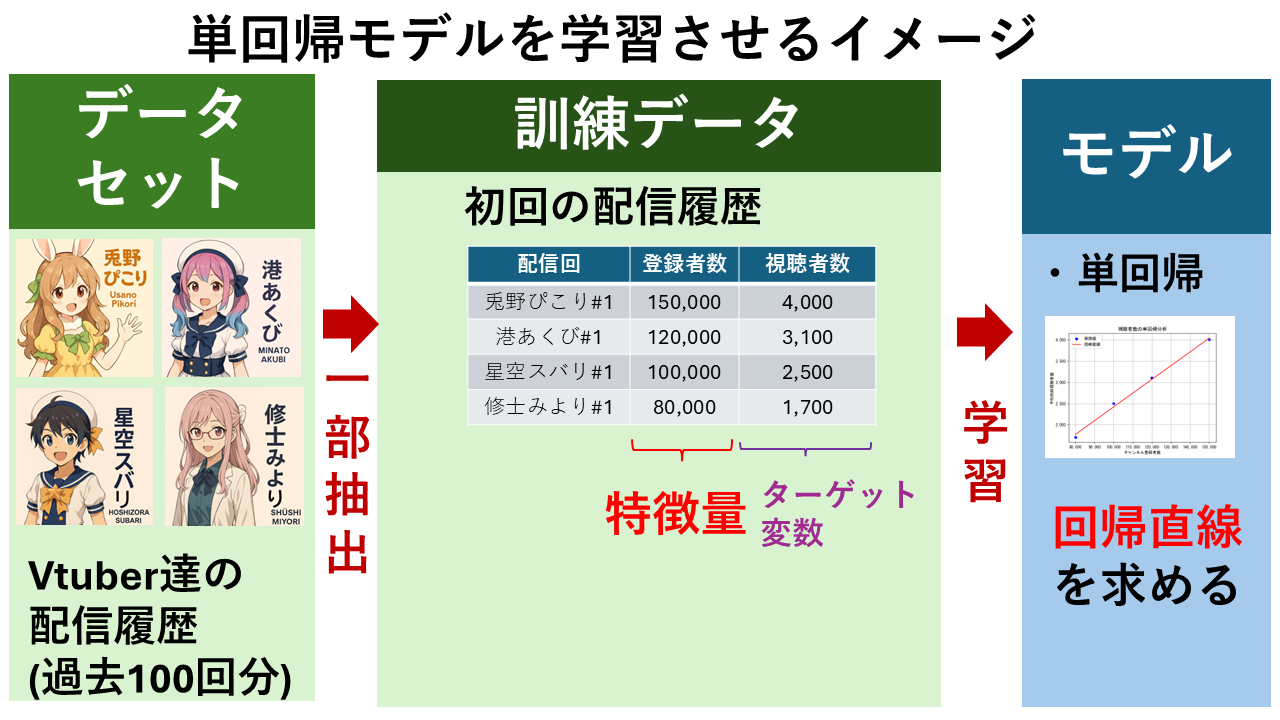
単回帰分析(Simple Linear Regression)は、1つの特徴量(x)から1つのターゲット変数(y)を予測するモデルです。数学的には以下の式で表されます。
予測値を計算する式:$ \hat{y} = ax + b $
実測値の関係:$ y = ax + b + \varepsilon $
| 変数 | 説明 | 例 |
|---|---|---|
| $ \hat{y} $ | モデルが計算したターゲット変数(目的変数)の推定値 | 視聴者数(予測値) |
| $ y $ | 実際に観測されたターゲット変数(目的変数)の値 | 視聴者数(実測値) |
| $ x $ | 特徴量(予測したい値に影響を与えるもの。説明変数ともいう) | チャンネル登録者数、Xのフォロワー数など(予測値) |
| $ a $ | 傾き($x$が1増えると$y$がどれだけ増えるか。重み、回帰係数ともいう) | 登録者数が1人増えたときの視聴者数の増加量 |
| $ b $ | 切片($x=0$のときの$y$の値) | 登録者数が0人のときの理論的な視聴者数 |
| $ ε $ | 誤差項(予測と実際のズレ) | 「モデルが説明できない部分」であり、ノイズや他の未考慮の要因を含みます。 |
予測値を計算する式$ \hat{y} = ax + b $は、「$x$に比例して$\hat{y}$が変化する関係」を表す、傾き$a$、切片$b$の一次関数です。グラフにすると以下のようなまっすぐな直線になります。この直線を「回帰直線」といいます。
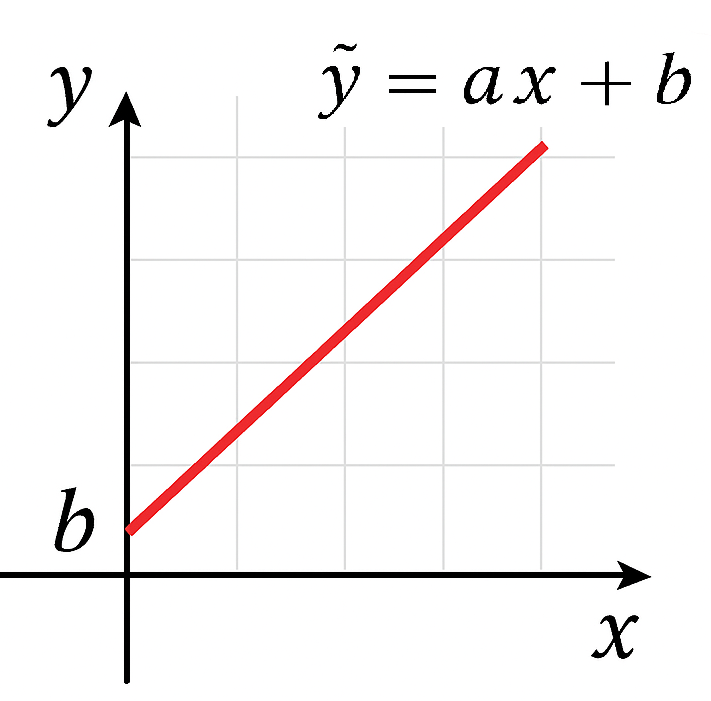
動画で見る
回帰直線
回帰直線の使い方

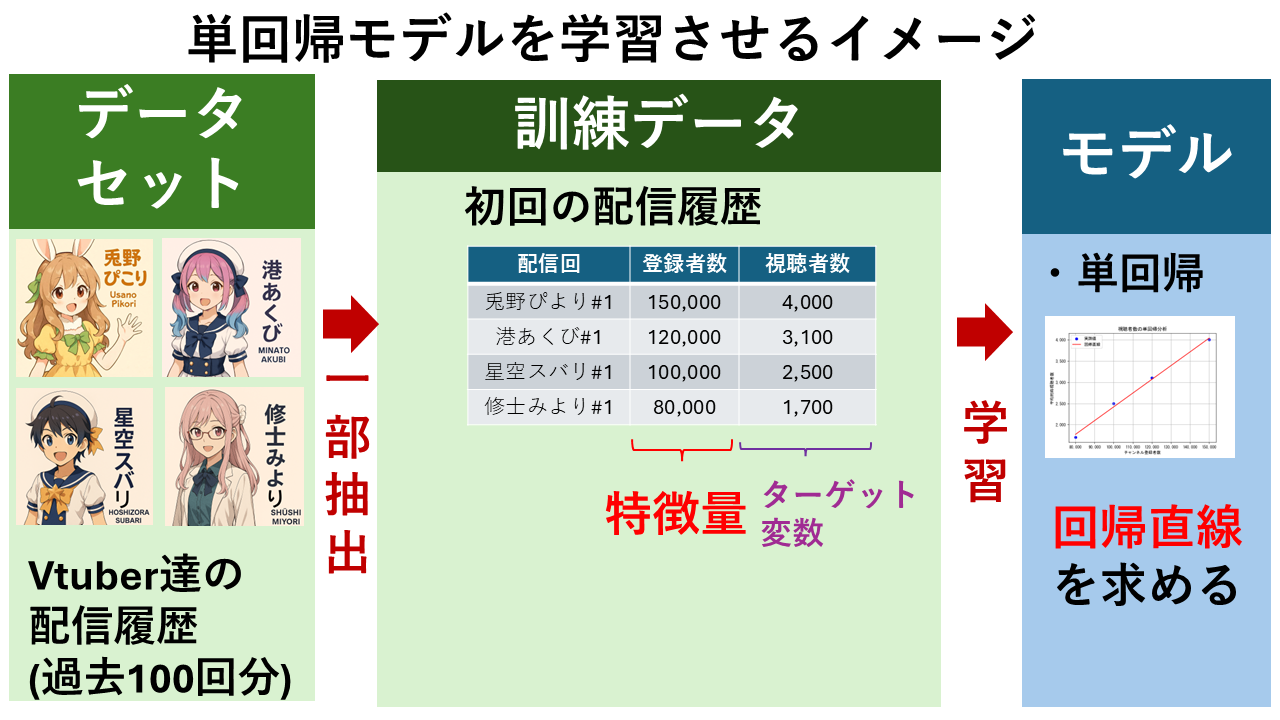
「VTuberの同時視聴者数を予測」することを例に、単回帰分析の計算式の意味と使い方を解説します。
例えば、以下のような4名のVTuberの初回配信における「チャンネル登録者数」と「視聴者数」の実測値のデータがあるとします。
| 配信回 | チャンネル登録者数(x) | 視聴者数(y) |
|---|---|---|
| 兎野ぺこり#1 | 150,000 | 4,000 |
| 港あくび#1 | 120,000 | 3,100 |
| 星空スバリ#1 | 100,000 | 2,500 |
| 修士みより#1 | 80,000 | 1,700 |
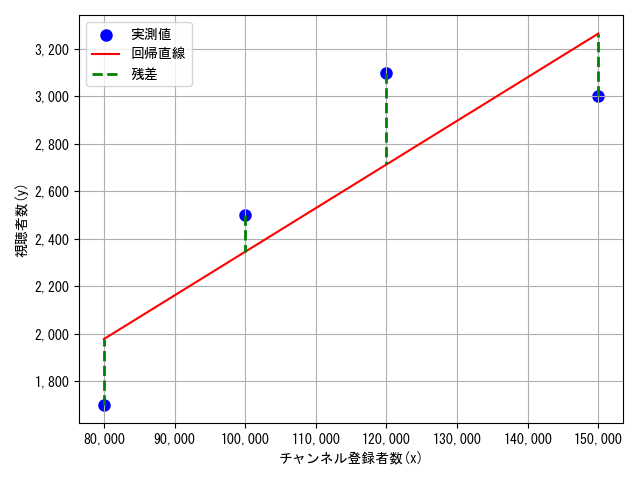
① チャンネル登録者数をx軸、視聴者数をy軸としたグラフに実測値をプロットします。(以下グラフの青い点が実測値)
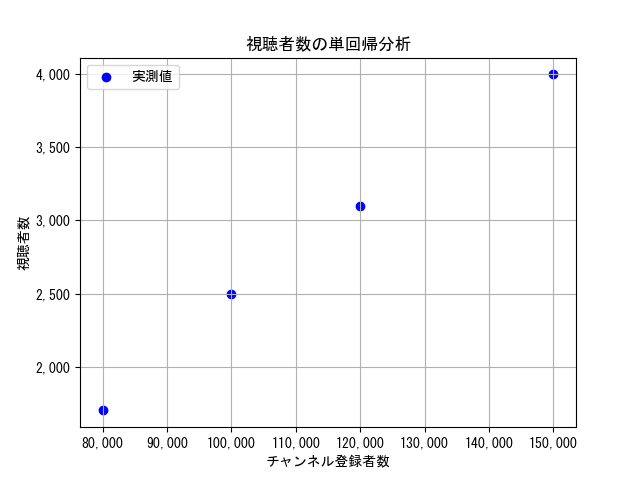
② プロットした点とのズレ(誤差)が最小になるような直線を引きます。この直線を回帰直線(赤色)といいます。
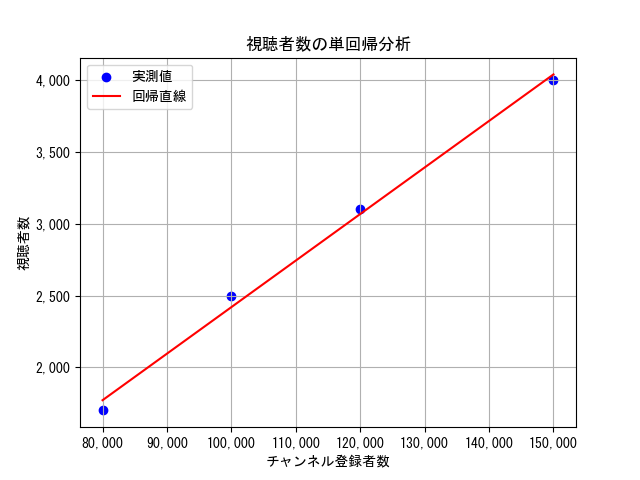
③ 回帰直線の傾き$a$と切片$b$を求めます。今回の例だと以下のようになります。
$ a = 0.03242990654205607 $
$ b = -823.3644859813076 $
④ 傾き$a$と切片$b$が求まれば、回帰直線の計算式が定まります。今回の例だと以下のようになります。(小数点第4位で切り捨て)
$ \hat{y} = 0.0324x -823.3644 $
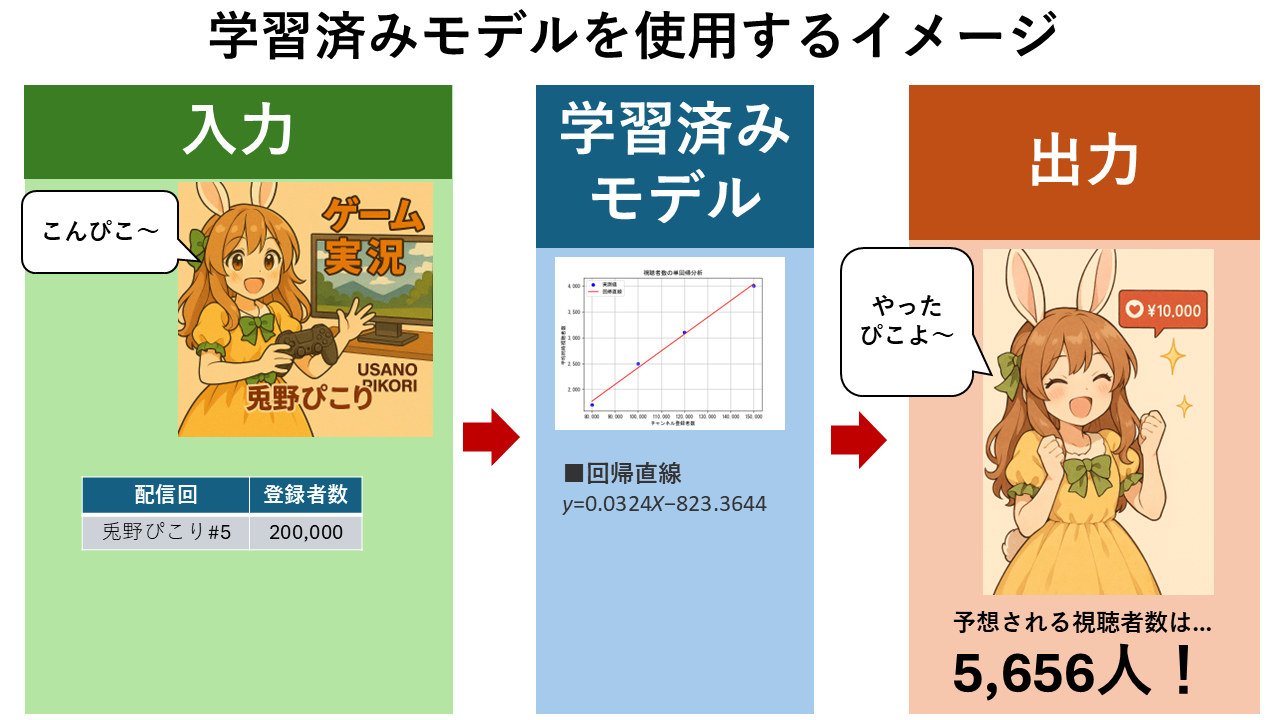
⑤ これで、「チャンネル登録者数」から「視聴者数」を予測することができるようになります。
例えば、「チャンネル登録者数」が20万人の場合、上記の計算式の $x = 200,000 $ となるので、
$ \hat{y} = 0.0324 \times 200,000 – 823.3644 = 5,656.6356 $
となります。つまり、チャンネル登録者数20万人の視聴者数の期待値(平均)は約5,656人と予測できます。
回帰直線の求め方(最小二乗法)
回帰直線の意味と使い方がわかったところで、具体的にどのように求めるのかを解説します。回帰直線を求めるには「最小二乗法(Least Squares Method)」という、データ点に最もよくフィットする直線を求める方法を用います。
① 最小二乗法では、残差(予測値と実測値の差)の二乗和を最小にするような直線$ \hat{y} = a x + b $を求めます。残差$e_i$の計算式は以下のようになります。
$ e_i = y_i – \hat{y_i} = y_i – (a x_i + b) = y_i – a x_i – b $
| 記号 | 意味 |
|---|---|
| $ i $ | データ点の番号(1番目、2番目…) |
| $ x_i $ | i番目の特徴量(例:チャンネル登録者数) |
| $ y_i $ | i番目のターゲット変数(例:視聴者数) |
| $ e_i $ | i番目の残差(予測と実測の差) |
| $ i $ | 配信回 | $ x_i $(i番目のチャンネル登録者数) | $ y_i $(i番目の視聴者数) |
|---|---|---|---|
| 1 | 兎野ぺこり#1 | $x_1=150,000$ | $y_1=4,000$ |
| 2 | 港あくび#1 | $x_2=120,000$ | $y_2=3,100$ |
| 3 | 星空スバリ#1 | $x_3=100,000$ | $y_3=2,500$ |
| 4 | 修士みより#1 | $x_4=80,000$ | $y_4=1,700$ |
② 残差の二乗和$S(a, b)$ の計算式は以下のようになります。
$S(a, b) = \sum_{i=1}^{n}e_i = \sum_{i=1}^{n} (y_i – a x_i – b)^2$
- $i$:各データ点の番号(1件目、2件目、…)
- $n$:データの総数(例:4件なら n = 4)
- $\sum_{i=1}^{n} e_i$:全データの残差の合計(予測値と実測値が完全に一致すれば0)
ズレを二乗することで、正負を打ち消さずに「どれだけ離れているか」を評価できます。
③ $ S(a, b) $ を $ a $ と $ b $ について偏微分し、0になる点を求めることで、最小値を計算します。
$ \frac{\partial S}{\partial a} = -2 \sum x_i (y_i – a x_i – b) = 0 $
$ \frac{\partial S}{\partial b} = -2 \sum (y_i – a x_i – b) = 0 $
④ 上記の連立式を$a$と$b$について解くと、以下の2つの式が得られます。
$ a = \frac{\sum (x_i – \overline{x})(y_i – \overline{y})}{\sum (x_i – \overline{x})^2} = \frac{S_{xy}}{S_x} $
$ b = \overline{y} – a \overline{x} $
| 変数 | 概要 | 意味 |
|---|---|---|
| $S_{xy}$ | $(x, y)$の共分散 | $x$と$y$がどれだけ一緒に変動するかを示す量。正なら同方向、負なら逆方向に動く傾向となる。 |
| $S_x$ | $x$の分散 | xのばらつきの大きさ。平均からどれだけ離れているかの平均的な量。 |
| $\overline{x}$ | $x$の平均 | xの値の合計をデータ数で割ったもの。xの中心的な値。 |
| $\overline{y}$ | $y$の平均 | yの値の合計をデータ数で割ったもの。yの中心的な値。 |
| $\sum $ | 総和(合計) | 添え字$i$と上限$n$が省略された略記。「$\sum_{i=1}^{n} a_i$」なら「$i = 1$から$n$まで、すべての$a_i$を足し合わせるという意味になる。 |
つまり、最小二乗法では、上記の計算式により回帰直線の傾き$a$と切片$b$を求めます。
回帰直線の計算例
それでは、先ほどの視聴者数を予測する回帰直線を手計算します。
| 配信回 | チャンネル登録者数(x) | 視聴者数(y) |
|---|---|---|
| 兎野ぺこり#1 | 150,000 | 4,000 |
| 港あくび#1 | 120,000 | 3,100 |
| 星空スバリ#1 | 100,000 | 2,500 |
| 修士みより#1 | 80,000 | 1,700 |
① 特徴量(チャンネル登録者数:x)とターゲット変数(視聴者数:y)の平均値を求めます。
$ \overline{x} = \frac{150{,}000 + 120{,}000 + 100{,}000 + 80{,}000}{4} = 112{,}500 $
$ \overline{y} = \frac{4{,}000 + 3{,}100 + 2{,}500 + 1{,}700}{4} = 2{,}825 $
② 特徴量の分散$S_x$ と共分散 $ S_{xy} $の計算に必要な値を求めます。
| 配信回 | i | $ x_i $ | $ y_i $ | $ x_i – \overline{x} $ | $ y_i – \overline{y} $ | $(x_i – \overline{x})(y_i – \overline{y})$ | $(x_i – \overline{x})^2$ |
|---|---|---|---|---|---|---|---|
| 兎野ぺこり#1 | 1 | 150,000 | 4,000 | 37,500 | 1,175 | 44,062,500 | 1,406,250,000 |
| 港あくび#1 | 2 | 120,000 | 3,100 | 7,500 | 275 | 2,062,500 | 56,250,000 |
| 星空スバリ#1 | 3 | 100,000 | 2,500 | -12,500 | -325 | 4,062,500 | 156,250,000 |
| 修士みより#1 | 4 | 80,000 | 1,700 | -32,500 | -1,125 | 36,562,500 | 1,056,250,000 |
③ 上記の結果より、特徴量の分散$S_x$ と共分散 $ S_{xy} $は以下のようになります。
$ S_{xy} = \sum (x_i – \overline{x})(y_i – \overline{y})=44,062,500+2,062,500+4,062,500+36,562,500=86,750,000 $
$ S_{x} = \sum (x_i – \overline{x})^2 $ = 1,406,250,000+56,250,000+156,250,000+1,056,250,000 = 2,675,000,000 $
④ 分散$S_x$ と共分散 $ S_{xy} $が求まれば、回帰直線の傾き$ a $ と切片 $ b $が求まります。
$ a = \frac{S_{xy}}{S_x} = \frac{86{,}750{,}000}{2{,}675{,}000{,}000} = 0.0324299065 $
$ b = \overline{y} – a \overline{x} = 2{,}825 – 0.0324299065 \times 112{,}500 = -823.364486 $
⑤ 小数第4位で切り捨てすると、回帰直線の式は以下のように求まります。
$ y = 0.0324x – 823.3644 $
切片 ≈ -823となっています。切片は、「登録者数が0人だった場合の理論的な視聴者数」を意味しますが、実際には「視聴者数がマイナスになる」ということはありえません。これは、モデルがデータの外側まで予測しようとしたために、現実とは合わない結果が出ています。こうした「データの外側での予測」は、正しくないことが多く、これを「外挿の限界」と呼びます。学習済みモデルのの予測値に対する信頼性が低下する領域であるため、注意が必要です。
相関係数
相関係数とは
相関係数 $r$ は、2つの変数の関係の強さを表す指標です。単回帰分析では「特徴量」と「ターゲット変数」の関係の強さを確かめることができます。つまり、「そもそも登録者数と視聴者数に関係があるのか?」ということを確認ができます。相関係数 $r$の範囲は −1〜+1 で、以下のように関係性の傾向を知ることができます。
| 相関係数 $r$ | 関係の強さ | 例 |
|---|---|---|
| $r = +1$ | 完全な正の相関 | 登録者数が増えると視聴者数も必ず増える |
| $r \approx +0.8$ | 強い正の相関 | 登録者数が増えると視聴者数も増える傾向がある |
| $r = 0$ | 無相関 | 登録者数と視聴者数に関係がない |
| $r \approx -0.8$ | 強い負の相関 | 登録者数が増えると視聴者数が減る傾向がある |
| $r = -1$ | 完全な負の相関 | 登録者数が増えると視聴者数が必ず減る |
相関係数の計算式
相関係数 $r$ は以下の式で求められます:
$$ r = \frac{S_{xy}}{\sqrt{S_x \cdot S_y}} $$
- $S_{xy}$:登録者数と視聴者数の共分散
- $S_x$:登録者数の分散
- $S_y$:視聴者数の分散
相関係数の計算例
回帰直線の計算例と同じデータで相関係数を求めてみます。
| 配信回 | チャンネル登録者数(x) | 視聴者数(y) |
|---|---|---|
| 兎野ぺこり#1 | 150,000 | 4,000 |
| 港あくび#1 | 120,000 | 3,100 |
| 星空スバリ#1 | 100,000 | 2,500 |
| 修士みより#1 | 80,000 | 1,700 |
① 回帰直線で既に求めた以下の値を使います。
- $S_{xy} = 86,750,000$
- $S_x = 2,675,000,000$
- $S_y = 1,827,500$(※視聴者数の分散)
② 相関係数を求める計算式に代入します。
$$ r = \frac{86,750,000}{\sqrt{2,675,000,000 \times 1,827,500}} \approx \frac{86,750,000}{2,211,000} \approx 0.9836 $$
③ 相関係数 $ r \approx 0.98 $ は非常に強い正の相関を示しており、登録者数が多いほど視聴者数も多い傾向があることがわかります。この場合、単回帰分析の見込みがありそうだと考えることができます。
訓練データに対する適合性
訓練データに対する適合性評価は、学習済みモデルが訓練用データにどれだけ合っているかを決定係数 $ R^2 $などの指標で評価することです。ただし、スコアが高すぎると、過学習の可能性もあるので注意が必要です。
決定係数
決定係数 $ R^2 $ は、回帰直線が実測値(訓練用データなど)にどれだけうまく沿っているかを示す指標です。決定係数$ R^2 $は 0〜1の範囲の値をとります。値が1に近いほど、実測値に近いと評価できます。
- $ R^2 = 1 $:すべての実測値が回帰直線上にあり、完全に再現できている。(理想的なモデル)
- $ R^2 \approx 0.8 $:実測値が回帰直線の付近にあり、高い予測精度がある。(実用的なモデル)
- $ R^2 = 0 $:実測値が回帰直線から大きく外れており、予測精度が低い。(不適なモデル)
決定係数の計算式
決定係数 $ R^2 $ は、以下の数式で計算できます。
$ R^2 = \frac{\text{SSR}}{\text{SST}} = 1 – \frac{\text{SSE}}{\text{SST}} $
※ $ \text{SST} = \text{SSR} + \text{SSE} $ の関係にあります。
| 項 | 概要 | 意味 |
|---|---|---|
| $ \text{SST} = \sum_{i=1}^{n} (y_i – \overline{y})^2 $ | 全体平方和(Total Sum of Squares) | 実測値 $ y_i $ が平均値 $ \overline{y} $ のまわりにどれだけ散らばっているかを示す。データ全体のばらつき。 |
| $ \text{SSR} = \sum_{i=1}^{n} (\hat{y}_i – \overline{y})^2 $ | 回帰平方和(Regression Sum of Squares) | 回帰式 $ \hat{y}_i = ax_i + b $ によって説明できたばらつき。予測値が平均からどれだけ離れているか。 |
| $ \text{SSE} = \sum_{i=1}^{n} (y_i – \hat{y}_i)^2 $ | 残差平方和(Error Sum of Squares) | 実測値と予測値のズレ(残差)の二乗和。回帰式では説明できなかった誤差。 |
| 記号 | 意味 |
|---|---|
| $ y_i $ | 実測値 |
| $ \hat{y}_i $ | 回帰直線による予測値 |
| $ \overline{y} $ | yの平均 |
| 分子 | 回帰式で説明できたばらつき(回帰平方和) |
| 分母 | データ全体のばらつき(全体平方和) |
決定係数の計算式は、「1 − 説明できなかった割合(残差平方和 ÷ 全体平方和)」、つまり「回帰直線が全体のばらつきのうち、何%を説明できたか」を表します。
- 回帰直線が実測値の散らばりにうまく沿っている → 説明力が高い($ R^2 $ が大きい)
- 回帰直線が実測値にほとんど合っていない → 説明力が低い($ R^2 $ が小さい)
また、決定係数を パーセンテージ表示したものを「寄与率」といいます。
$ \text{寄与率} = R^2 \times 100\% $
決定係数の計算例
それでは、先ほど手計算した回帰直線の決定係数を手計算します。
| 配信回 | チャンネル登録者数(x) | 視聴者数(y) |
|---|---|---|
| 兎野ぺこり#1 | 150,000 | 4,000 |
| 港あくび#1 | 120,000 | 3,100 |
| 星空スバリ#1 | 100,000 | 2,500 |
| 修士みより#1 | 80,000 | 1,700 |
① 計算に必要な値を計算します。
| $i$ | $ x_i $ | $ y_i $ | $ \hat{y}_i $ | $ y_i – \hat{y}_i $ | $ (y_i – \hat{y}_i)^2$ |
|---|---|---|---|---|---|
| 1 | 150,000 | 4,000 | 3,961.48 | 38.52 | 1,484.83 |
| 2 | 120,000 | 3,100 | 3,062.22 | 37.78 | 1,426.66 |
| 3 | 100,000 | 2,500 | 2,419.63 | 80.37 | 6,460.17 |
| 4 | 80,000 | 1,700 | 1,776.05 | -76.05 | 5,785.62 |
② 残差平方和(SSE)を計算します。
$ \text{SSE} = 1,484.83 + 1,426.66 + 6,460.17 + 5,785.62 = 15,157.28 $
③ 全体平方和(SST)を計算します。
| $ y_i $ | $ y_i – \overline{y} $ | $ (y_i – \overline{y})^2 $ |
|---|---|---|
| 4,000 | 1,175 | 1,380,625 |
| 3,100 | 275 | 75,625 |
| 2,500 | -325 | 105,625 |
| 1,700 | -1,125 | 1,265,625 |
$ \text{SST} = 1,380,625 + 75,625 + 105,625 + 1,265,625 = 2,827,500 $
④ よって、決定係数$ R^2 $ は以下のように計算できます。
$ R^2 = 1 – \frac{\text{SSE}}{\text{SST}} = 1 – \frac{15,157.28}{2,827,500} \approx 0.9946 $
回帰直線は 99.46% のばらつきを説明できているため、訓練データに対してうまくフィットしていることがわかります。
残差分析
残差分析は、学習済みモデル(回帰直線)の妥当性を評価するために、予測値と実測値の差(残差)を調べる手法です。
具体的には、求めた残差を使って「残差プロット」や「残差ヒストグラム」を作成して視覚的に確認したり、検定という統計的な手法を用いて数値的に確認したりします。残差分析でチェックする主なポイントは以下のとおりです。
① 残差がX軸全体にランダムに分布しているか? → ランダムに分布していれば、モデルの線形性・等分散性が保たれている
② 特定のパターン(曲線・広がりの変化)がないか? → パターンがあれば、モデルが非線形か、変数変換が必要かも
③ 赤い水平線(y=0)を中心に上下にバラけているか?
【残差ヒストグラムの確認ポイント】
① ヒストグラムが左右対称のベル型になっているか? → ベル型なら残差が正規分布に近い(線形回帰の前提条件を満たす)
② 外れ値(極端な残差)が多すぎないか? → 歪み・尖り・裾が広いと、モデルの見直しやロバスト回帰の検討が必要かも
※正規性検定(Shapiro-Wilk)と合わせて、視覚的に正規分布かどうかを判断する材料になる
【例】

例えば、上記だと、線形回帰モデルの前提(線形性・等分散性)をおおむね満たしているが、残差のばらつきが広く、一部の予測が大きく外れている(訓練データに大きな外れ値)が含まれている可能性があると判断できます。
| 観点 | 解釈 |
|---|---|
| 線形性 | 残差がランダムに分布 → OK |
| 分布の形状(等分散性) | 残差の広がりがやや右寄り(正の残差が多い) → 実測値 < 予測値が多い(過大予測) |
| 最頻値が +200 付近 | 一部の予測が大きく外れている可能性あり |
| 左右対称性(正規性) | やや右寄りで完全な正規分布ではないが、極端な歪みはない。統計的にはOK(p値 > 0.05) |
| 裾の広がり | -300〜+200 → 誤差の範囲が広く、一部の予測が大きく外れている可能性あり |
汎化性能の検証
汎化性能とは
汎化性能とは、学習済みモデルが未知のデータに対してどれだけ正確に予測できるかというものです。
つまり、「訓練データ」から作成した回帰直線が、訓練では未使用の新しいデータに対しても有効かどうかを確認します。汎化性能が低い場合は、「過学習対策」を検討する必要があります。
検証の流れ
- 訓練では未使用の新しいデータで構成された「テストデータ」を作成します。
- 例:作り方に決まりはありませんが、元のデータセットから80%を訓練用、20%をテスト用として使うことが多いです。注意点として、訓練用とテスト用は分ける必要があります。
- 「学習済みモデル」に「テストデータ」を入力し、予測を行います。
- 「テストデータ」の特徴量 $x_{\text{test}}$ を学習済みモデルに入力し、予測値 $\hat{y}_{\text{test}}$ を取得します。
- 精度の評価します。
- 実際の値 $y_{\text{test}}$ と予測値 $\hat{y}_{\text{test}}$ を比較し、誤差を計算します。
- 誤差を使って、平均絶対誤差(MAE)、平均二乗誤差(MSE)、MSEの平方根(RMSE)、決定係数$R^2$などの指標を求め、性能を評価します。
- 決定係数は訓練データに対してうまくフィットしているかだけでなく、テストデータに対してうまくフィットしているかの指標にも用いることができます。
| 指標名 | 意味 | 数値の見方 |
|---|---|---|
| MAE (Mean Absolute Error) |
予測値と実測値の「平均的なズレ」、「予測が毎回どれくらい外れるか」 | 小さいほど良い 例:MAE = 300 → 平均300人ズレてる |
| MSE (Mean Squared Error) |
誤差を2乗して平均化(大きな誤差に厳しい) | 小さいほど良い 例:MSE = 90,000 → 誤差の2乗平均が9万 |
| RMSE (Root Mean Squared Error) |
MSEの平方根(単位が元データと同じ)、誤差の平均的な大きさを直感で把握 | 小さいほど良い 例:RMSE = 300 → MAEと同じくらいなら安定 |
| $R^2$(決定係数) | テストデータに対する説明力 | 1に近いほど良い。 |
平均絶対誤差(MAE)は以下の計算式で求めます。
$ \text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i – \hat{y}_i| $
平均二乗誤差(MSE)は以下の計算式で求めます。
$ \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i – \hat{y}_i)^2 $
二乗平均平方根誤差(RMSE)は以下の計算式で求めます。
$ \text{RMSE} = \sqrt{\text{MSE}} = \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (y_i – \hat{y}_i)^2 } $
決定係数$R^2$は以下の計算式で求めます。
$ R^2 = \frac{\text{SSR}}{\text{SST}} = 1 – \frac{\text{SSE}}{\text{SST}} $
※ $ \text{SST} = \text{SSR} + \text{SSE} $ の関係にあります。
| 項 | 概要 | 意味 |
|---|---|---|
| $ \text{SST} = \sum_{i=1}^{n} (y_i – \overline{y})^2 $ | 全体平方和(Total Sum of Squares) | 実測値 $ y_i $ が平均値 $ \overline{y} $ のまわりにどれだけ散らばっているかを示す。データ全体のばらつき。 |
| $ \text{SSR} = \sum_{i=1}^{n} (\hat{y}_i – \overline{y})^2 $ | 回帰平方和(Regression Sum of Squares) | 回帰式 $ \hat{y}_i = ax_i + b $ によって説明できたばらつき。予測値が平均からどれだけ離れているか。 |
| $ \text{SSE} = \sum_{i=1}^{n} (y_i – \hat{y}_i)^2 $ | 残差平方和(Error Sum of Squares) | 実測値と予測値のズレ(残差)の二乗和。回帰式では説明できなかった誤差。 |
RMSEが大きい場合、学習済みモデルが外れ値に弱い可能性があります。決定係数$R^2$が訓練データに対しては大きく、逆にテストデータに対して小さい場合、**過学習**になっている可能性があります。
K分割交差検証
交差検証(Cross Validation)は、モデルの汎化性能(未知データへの強さ)を評価するためのテスト方法の1つです。 データを複数の「訓練用」と「検証用」に分割して、モデルを何度も学習・評価することにより、評価の偏りを平均化し、信頼性を向上させます。先程の例では、訓練データとテストデータに分割して性能評価をしていますが、K分割交差検証(K-Fold Cross Validation)を使うことで、より安定した汎化性能の評価が可能になります。
交差検証のやり方はいくつかありますが、今回は代表的な方法である「K分割交差検証(K-Fold Cross Validation)」を行います。
- データを K個のグループ(fold) に分割する
- 各回で、K-1個を訓練用、残り1個を検証用としてモデルを学習・評価する
- これを K回繰り返す(foldを順番に検証用にする)
- 最終的に、K回の評価結果の平均を取る
例えば、K=5 の場合、以下のようになります。
- データを5分割(Fold1〜Fold5)
- 各回で1つのfoldを検証用、残り4つを訓練用に使う
- 5回繰り返して、平均的な性能を評価
| 回 | 訓練データ | 検証データ |
|---|---|---|
| ① | Fold2〜5 | Fold1 |
| ② | Fold1,3〜5 | Fold2 |
| ③ | Fold1,2,4,5 | Fold3 |
| ④ | Fold1〜3,5 | Fold4 |
| ⑤ | Fold1〜4 | Fold5 |
Pythonプログラミングによる実装例を以下ページで詳しく解説しています。

予測の不確かさ
「信頼区間」と「予測区間」とは
単回帰分析では、ある特徴量$ x $ に対してターゲット変数 $ y $ を予測する回帰直線を求めますが、その予測値がどれくらい確かなものなのかを知ることが重要です。たとえば、登録者数が20万人のVTuberに対して「視聴者数は約5,656人」と予測できたとしても、
- その予測値はどれくらいの誤差を含んでいるのか?
- 実際の視聴者数はどの範囲に収まりそうか?
- モデルの予測は平均的にどれくらい信頼できるのか?
といった疑問が生じます。こうした予測の不確かさを定量的に評価するために、「信頼区間」や「予測区間」が用いられます。
| 区間 | 意味 | 例(視聴者数の予測) |
|---|---|---|
| 信頼区間(Confidence Interval) | 回帰直線の平均的な予測値がどの範囲にあるかを示す | 「登録者数20万人のVTuberの平均的な視聴者数は、5,600〜5,700人の間にあると考えられる」 |
| 予測区間(Prediction Interval) | 個々のデータ点の実際の視聴者数がどの範囲にあるかを示す | 「登録者数20万人のVTuberの実際の視聴者数は、4,800〜6,400人の間になる可能性がある」 |
「信頼区間」と「予測区間」の計算式
回帰直線 $ \hat{y} = ax + b $の「ある特徴量の値 $ x_0 $ 」に対する予測値 $ \hat{y}_0 $ に対して、信頼区間の範囲は以下の式で計算できます。
$$ \hat{y_0} \pm W_{CI} $$
$$ W_{CI} = t_{\alpha /2, n-2} \cdot s \cdot \sqrt{ \frac{1}{n} + \frac{(x_0 – \bar{x})^2}{\sum (x_i – \bar{x})^2} } $$
また、予測区間の範囲は以下の式で計算できます。
$$ \hat{y_0} \pm W_{PI} $$
$$ W_{PI} = t_{\alpha /2, n-2} \cdot s \cdot \sqrt{ 1 + \frac{1}{n} + \frac{(x_0 – \bar{x})^2}{\sum (x_i – \bar{x})^2} } $$
| 記号 | 意味 |
|---|---|
| $ s $ | 残差の標準誤差(RMSE) |
| $ t_{\alpha/2, n-2} $ | t分布の臨界値 |
| $ n $ | データ数 |
| $ \bar{x} $ | 特徴量(説明変数)の平均 |
ここで、信頼区間と予測区間に関する重要なキーワードをいくつか解説します。
t値は、t分布という統計分布から得られる値で、主に以下のような場面で使われます。
① 母集団の標準偏差が不明(≠既知)で、サンプルから推定する場合
② サンプルサイズが小さい(通常30未満)
③ 回帰分析や平均の信頼区間を求めるとき
通常、サンプル数が大きいと「標準正規分布(Z分布)」を使います。サンプル数が小さいとばらつきが大きくなるため、より広がった分布=t分布を使います。t分布は、自由度によって形が変わります。
母集団(population)とは、調査や分析の対象となるすべてのデータの集合のことです。
(例)
VTuberの視聴者数を分析するなら → 「すべてのVTuber」のデータが母集団
星の明るさを測定するなら → 「観測可能なすべての星」が母集団
標本(サンプル)とは、母集団から選んだ一部のデータのことです。
(例)
VTuberの視聴者数を分析するなら →4人のVTuberの視聴者数
星の明るさを測定するなら → 「20個の星」が母集団
現実には、母集団全体を調べるのは困難です。そのため、 一部のデータ(標本)を使って母集団の性質(平均、分散、傾向など)を推定するのが基本的な考え方です。
自由度は、「自由に変動できるデータの数」のことです。たとえば、平均を計算するときに1つの値が決まると、残りの値は平均を保つために制約されます。つまり、制約の数だけ自由度が減るといえます。
(計算式)
$ \text{自由度} = n – p $
$ n $:データ点の数(標本サイズ)
$ p $:推定したパラメータの数(回帰係数の数)
今回の視聴者数予測では、データ数は4つ($n=4$)、推定したパラメータは2つ(傾き$a$と切片$b$)なので、自由度は$2$となります。
「母集団の真の値がこの区間に含まれる確率が95%」という意味です。自由度2での95%信頼水準の両側t値は「4.303」です。この値は、信頼区間や予測区間の誤差幅を拡張する係数として使います。「4.303」という数値は、t分布表から自由度「df = 2」の行、「0.025(片側2.5%)」の列から抽出できます。
「信頼区間」と「予測区間」の計算例
上記で求めた視聴者数を予測する回帰直線の信頼区間と予測区間を求めます。
| 項目 | 値 |
|---|---|
| 回帰式 | ( y = 0.0324x – 823.3644 ) |
| $ x_0 $(予測対象) | 200,000 |
| $ \bar{x} $(特徴量$x$の平均) | 112,500 |
| $ n $(データ数) | 4 |
| $ \sum (x_i – \bar{x})^2 $ | 2,675,000,000 |
| 残差標準誤差 $ s $ | 約61.3(※後述) |
| t値(95%信頼水準, 自由度2) | 約4.303(※t分布表より) |
① 予測値を計算します。
$ \hat{y}_0 = 0.0324 \times 200,000 – 823.3644 = 6,480 – 823.3644 = 5,656.6356 $
② 信頼区間の誤差幅を以下の式で計算します。
$ W_{CI} = t \cdot s \cdot \sqrt{ \frac{1}{n} + \frac{(x_0 – \bar{x})^2}{\sum (x_i – \bar{x})^2} } = 4.303 \cdot 61.3 \cdot 1.763 \approx 466.2 $
- $ x_0 – \bar{x} = 87,500 $
- $ \frac{(x_0 – \bar{x})^2}{\sum (x_i – \bar{x})^2} = \frac{7.65625 \times 10^9}{2.675 \times 10^9} \approx 2.8617 $
- $ \frac{1}{n} = 0.25 $
- 合計:$ \sqrt{0.25 + 2.8617} \approx \sqrt{3.1117} \approx 1.763 $
③ 予測区間は「信頼区間の式」にさらに「+1」を加えた分だけ広くなります。
$ W_{PI} = t \cdot s \cdot \sqrt{ 1 + \frac{1}{n} + \frac{(x_0 – \bar{x})^2}{\sum (x_i – \bar{x})^2} } = 4.303 \cdot 61.3 \cdot 2.0278 \approx 535.6 $
- $ 1 + 0.25 + 2.8617 = 4.1117 $
- $ \sqrt{4.1117} \approx 2.0278 $
④ よって、「信頼区間」と「予測区間」は以下のとおりになります。
| 区間 | 範囲 | 解釈 |
|---|---|---|
| 信頼区間 | 5,190.4 ~ 6,122.8人 | 登録者数20万人の平均的な視聴者数の予測範囲(95%の確率でこの範囲に収まる) |
| 予測区間 | 5,121.0 ~ 6,192.2人 | 登録者数20万人の実際の視聴者数が入る可能性のある範囲(95%の確率でこの範囲に収まる) |
- $ \hat{y_0} – W_{CI} = 5,656.6 – 466.2 = 5,190.4 $
- $ \hat{y_0} + W_{CI} = 5,656.6 + 466.2 = 6,122.8 $
- $ \hat{y_0} – W_{PI} = 5,656.6 – 535.6 = 5,121.0 $
- $ \hat{y_0} + W_{PI} = 5,656.6 + 535.6 = 6,192.2 $
プログラミングによる実装方法
Pythonライブラリ「Scikit-learn」を用いた単回帰分析の実装方法について、以下ページで解説しています。

まとめ
単回帰分析は、1つの特徴量(説明変数)から1つのターゲット変数(目的変数)を予測するための基本的な手法です。単回帰分析を行うときの基本的な流れは以下のとおりです。
- 相関係数で関係性を確認
- 単回帰分析を始める前に、特徴量$x$とターゲット変数$y$に強い関係があるかを確認します。
- 相関係数$r$を計算し、非常に強い正の相関があれば、単回帰分析に適していると判断できます。
- データの準備
- 訓練データとして、特徴量$x$とターゲット変数$y$のペアを用意します。
- 回帰直線の計算
- 最小二乗法を用いて、傾き$a$と切片$b$を求め、回帰式$y = ax + b$を求めます。
- 訓練データに対する適合性評価
- 決定係数$R^2$を使って、回帰直線がどれだけ訓練データ(実測値)にフィットしているかを確認します。
- *残差分析による学習済みモデルの評価🧪
- 残差$e_i = y_i – \hat{y}_i$を計算し、以下の観点などから学習済みモデルの妥当性を確認します。
- 残差プロット・ヒストグラムから残差がランダムに分布しているか視覚的に確認(非線形性・外れ値・分散不均一性の検出)
- Shapiro-Wilk検定やQ-Qプロットで残差が正規分布に従うかを確認
- 汎化性能の検証
- テストデータに対して予測を行い、MAE・MSE・RMSE・$R^2$などの指標で精度を評価します。
- 予測の不確かさの理解
- 信頼区間と予測区間を用いて、予測値のばらつきや誤差の範囲を定量的に把握します。
ただし、以下の「前提条件」が整っていないと精度が悪くなります。
- 変数同士の関係が直線的(線形)であること
- たとえば、登録者数が2倍になったら視聴者数も2倍になるような相関関係があるかどうか
- 誤差のばらつきが一定であること(等分散性)
- 登録者数が少ない人と多い人で、予測の精度に差が出すぎていないか
- 外れ値(極端に大きい or 小さい値)が訓練データに含まれていると、回帰直線が一部のデータに引っ張られて、全体的に過大・過小予測するようになる
関連ページ
以下のページでは、機械学習の様々な手法を理論的に学ぶことができます。
以下のページでは、Pythonライブラリ「Scikit-learn」を用いた機械学習の実装方法を学ぶことができます。


コメント