二分法のアルゴリズムとプログラムの実装方法について解説します。
二分法
二分法とは、数値計算的に方程式の近似解を求めるアルゴリズムの1つです。
つまり、f(x)=0になるxを求めることができます。
アルゴリズム
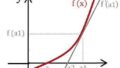
関数f(x)の符号が異なるように、2つのxの値(aとb)を選びます。
このとき、以下の式が成立します。
(1) ![]()
このとき、最初の近似解mは以下のようになります。
(2) ![]()
以下の式が成立する場合は、真値より右側にあることになります。
(3) ![]()
その際は、bにmの値を代入します。
そうでない場合、近似解は、真値より左側にあるので、aにmの値を代入します。
そして、更新されたa、bを用いて、再び近似解mの値を計算します。
これを繰り返していき、a、bが解の真値から同じ分だけ離れた場合、mは真値となります。
方程式が連続関数で、関数値の符号が異なる初期条件を与えると、必ず収束して解を導出できます。
関数が単調増加・減少の場合は、区間上限を十分大きく、区間下限を十分小さくすることで適切な初期条件が得られます。
プログラムの実装例
プログラミングによる実装例は下記事で紹介しています。

【C言語】二分法のプログラム
この記事では、C言語で二分法により方程式の解を解を求めるプログラムについてソースコード付きで解説します。

【Python】二分法のプログラム
この記事では、Python言語で二分法により方程式の解を求めるプログラムについてソースコード付きで解説します。

【Java】二分法のプログラム
この記事では、Javaで二分法を実装する方法についてソースコード付きで紹介します。

【C#】二分法のプログラム
この記事では、C#言語で二分法により方程式の解を解を求めるプログラムについてソースコード付きで解説します。

【Javascript】二分法のプログラム
この記事では、Javascript言語で二分法により方程式の解を求めるプログラムについてソースコード付きで解説します。

コメント