【オイラー法】アルゴリズム・プログラム

オイラー法のアルゴリズムとプログラムの実装方法について解説します。

オイラー法

オイラー法(Euler Method)とは、数値計算的に常微分方程式の近似解を求めるアルゴリズムの1つです。
このアルゴリズムを使うことで、例えばRLC回路の過渡応答や、マスダンパバネ系の応答の計算をプログラミングで行うことができます。

1階の常微分方程式を初期条件x(t0)=x0、区間[t0, tn]の下で解くことを考えます。
このとき、導関数の定義は

(1) $\begin{eqnarray*} \frac{dx}{dt}=\lim_{h \to 0} \frac{x(t+h)-x(t)}{h} \end{eqnarray*}$

となります。hが十分小さいときは

(2) $\begin{eqnarray*} \frac{dx}{dt}=\lim_{h \to 0} \frac{x_{i+1}-x_i}{h} \end{eqnarray*}$

と考えることにより、

(3) $\begin{eqnarray*} x_{i+1}=x_i+hf(x_i, t_i) \end{eqnarray*}$

となります。したがって

(4) $\begin{eqnarray*} x_1=x_0+hf(x_0, t_0) \\ x_2=x_1+hf(x_1, t_1) \\ ... \\ x_n=x_{n-1}+hf(x_{n-1}, t_{n-1}) \end{eqnarray*}$

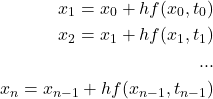
※nは計算回数
つまり、上記の式で計算を順番に繰り返していくと、任意の時間tのときのx(t)を求めることが出来ます。

プログラミングによる実装例は下記事で紹介しています。

プログラミングによる実装例は下記事で紹介しています。