この記事では、ベクトルの外積の計算式について解説します。
## 内積の計算式
2つの空間ベクトル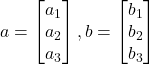 の外積は次式で計算できます。
の外積は次式で計算できます。
(1) 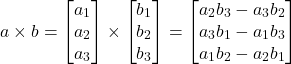
## 覚え方(たすき掛け)
式をそのまま覚えるのはつらいです。
そこでよくある覚え方が「たすき掛け」というものです。
①外積の1行目の値は、ベクトルa, bの2行目と3行目をたすき掛けするようにして計算します。
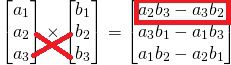
②外積の2行目の値は、ベクトルa, bの3行目と1行目をたすき掛けするようにして計算します。
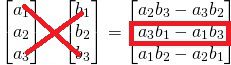
③外積の3行目の値は、ベクトルa, bの1行目と2行目をたすき掛けするようにして計算します。
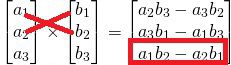
このように、外積を計算する時は
「求める行以外のベクトルa, bの2つの行をたすき掛けする」
という風に覚えておけば式を丸暗記する必要がなく楽です。
【関連記事】
線形代数入門

コメント