ニューラルネットワーク(多層パーセプトロン・MLP)や特徴や原理、その計算方法についてまとめました。
多層パーセプトロン(MLP)とは
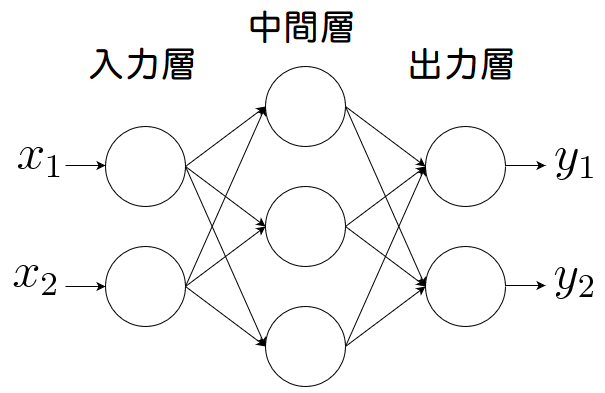
多層パーセプトロン(MLP)とは、下図のように(単純)パーセプトロンを複数繋いで多層構造にしたニューラルネットです。
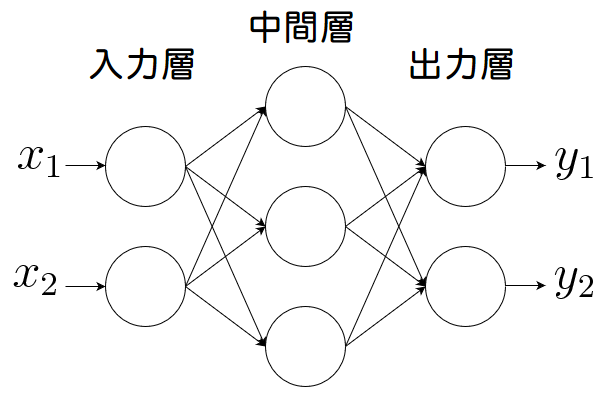
左から入力層、中間層(隠れ層)、出力層と呼ばれます。
この場合は3層構造なので「3層パーセプトロン」とも呼ばれます。
ユニット数や層数は決まっているわけではありません。
そのため、例えば入力層のユニット数を3以上に増やしたり、中間層の階層数を2つにして4層構造にすることも可能です。
作成するモデルによってユニット数や階層数を調整します。
ニューラルネットワークとは?基本原理と活性化関数、単純パーセプトロンについて徹底解説
ニューラルネットワークとは?基本原理と活性化関数、単純パーセプトロンについてまとめました。ニューラルネットワークとは脳内には、ニューロン(神経細胞)が無数にあります。ニューロン同士はシナプスで繋がっています。入力される電気信号の電位がある閾...
確率的勾配降下法
多層パーセプトロンでは、「確率的勾配降下法」で重みを更新します。
(1) 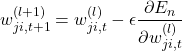
| パラメータ | 説明 |
|---|---|
| 目的関数 |
2乗誤差。目的関数が最小になるときの重みを求める。 |
| 学習率(重みの学習速度を決定するパラメータ) |
誤差逆伝播により、![]() を計算できます。
を計算できます。
出力層の重み更新
2乗誤差![]() を出力層の重み
を出力層の重み![]() で偏微分すると次のようになります。
で偏微分すると次のようになります。
(2) 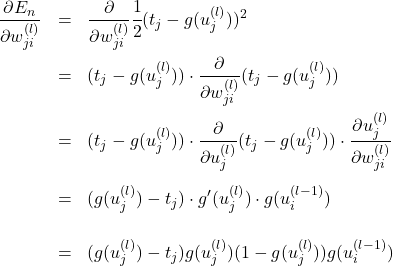
| パラメータ | 説明 |
|---|---|
| 教師データ。 | |
| 活性化関数 |
|
| 活性化関数の微分 |
中間層の重み更新
2乗誤差 ![]() を中間層の重み
を中間層の重み ![]() で偏微分すると次のようになります。
で偏微分すると次のようになります。
(3) 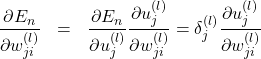
右辺第1項は次のようになります。
(4) 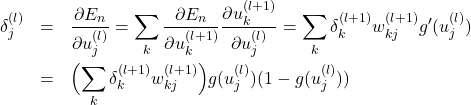
右辺第2項は次のようになります。
(5) 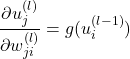
よって
(6) 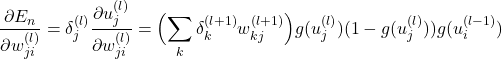
中間層![]() の重みを更新するときは、その次の層
の重みを更新するときは、その次の層![]() の
の![]() が必要となります.
が必要となります.
出力層での![]() は、出力値と教師の差から求まります。
は、出力値と教師の差から求まります。
これを出力層から入力層の方向に順番に伝播させることで中間層の重みを更新します。
【活性化関数】中間層はReLU関数、出力層付近はソフトマックス関数
| – | – |
|---|---|
| 中間層 | 勾配消失問題が発生しくく、簡単なためReLU(ランプ関数)がよく用いられる。(以前は0~1に値を正規化するシグモイド関数が使われていたが、勾配消失問題が発生しやすいため現在はあまり使われない) |
| 出力層付近 | ソフトマックス関数がよく用いられる。 |
https://algorithm.joho.info/machine-learning/tutorial-ml/

コメント
①確率的勾配降下法は自らの重みを変えることであり次の層の重みを変えるものではありません。
②パラメタの説明のuは上式には関係ありません。
※donaldkaoki様
コメントありがとうございます。
該当箇所を修正致しました。
「確率的勾配降下法」において完全に勘違いしており、大変勉強になりました。