ニューラルネットワークとは?基本原理と活性化関数、単純パーセプトロンについてまとめました。
ニューラルネットワークとは
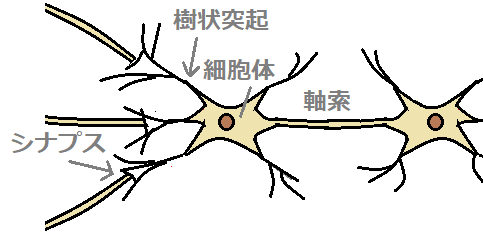
脳内には、ニューロン(神経細胞)が無数にあります。ニューロン同士はシナプスで繋がっています。
入力される電気信号の電位がある閾値を超えると発火し、シナプスによって次のニューロンに電気信号を出力します。
この動作を各ニューロンへ繰り返ししていくことで、脳は電気信号(情報)を伝達します。
ニューラルネットワークでは、この「脳が電気信号(情報)を伝達する仕組み」を表現することを目指した数学モデルです。
モデル図
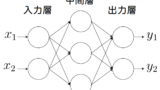
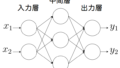
■ニューロン(左)、数学モデル(右)
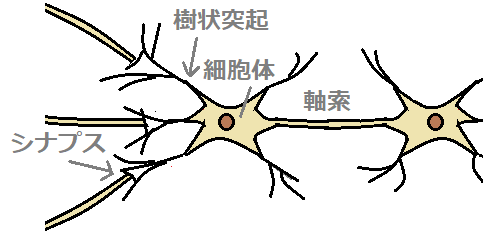
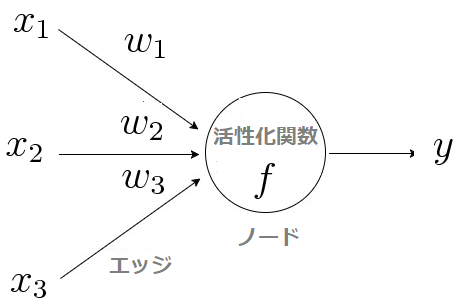
ニューロンモデルでは、細胞体を「ノード」、軸索を「エッジ」、シナプスを「活性化関数」で表現します。
| ニューロン | 数学モデル | 役割 |
|---|---|---|
| 入力信号 | 入力値 | |
| 出力信号 | 出力値 | |
| 軸索 | エッジ | 入出力端子 |
| 樹状突起 | 結合荷重 |
シナプスそれぞれがもつ信号の伝達効率 |
| 細胞体 | ノード(活性化関数 |
①入力の重み付き和を計算 ②計算結果が閾値を超えたら「1」、そうでなければ「0」を出力 |
重み付き総和
入力の重み付き総和![]() は以下の式で計算します。
は以下の式で計算します。
(1) 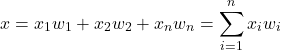
活性化関数
活性化関数では、重み付き和![]() がある閾値を超えていれば「1」、そうでなければ「0」を出力するように設計します。
がある閾値を超えていれば「1」、そうでなければ「0」を出力するように設計します。
これは、電気信号がある電位を超えた時に急激に発火するニューロンの特性を表現したものです。
活性化関数としてよく利用される関数は次の通りです。
| 関数名 | 関数 |
|---|---|
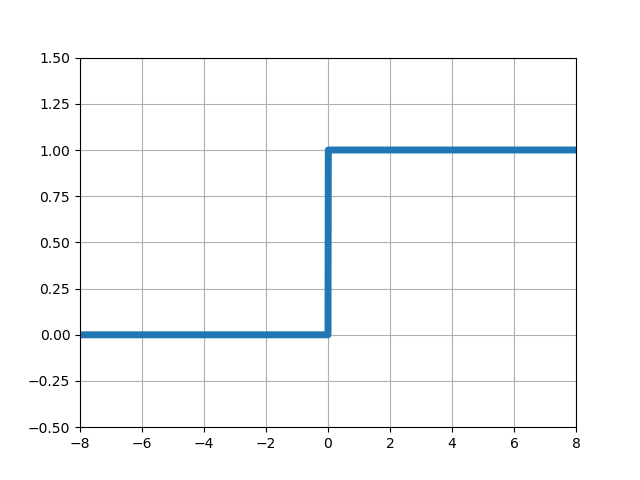
| ステップ関数 (ヘビサイド関数、階段関数) |
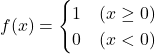 |
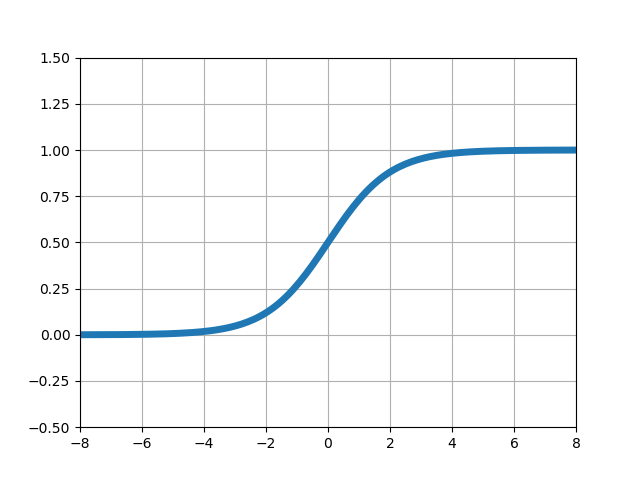
| シグモイド関数 | |
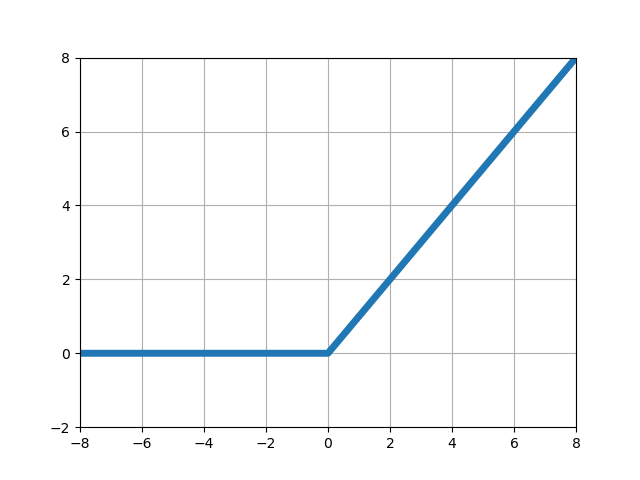
| 線形ランプ関数 |
![]() はある閾値です。
はある閾値です。
■左からステップ関数、シグモイド関数、ランプ関数
単純パーセプトロン
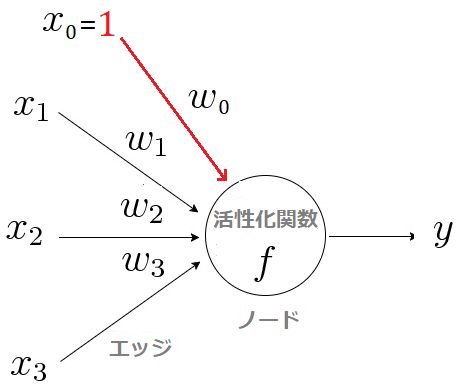
単純パーセプロトンとは、0番目の入力![]() を1、重み
を1、重み![]() を閾値とした場合のニューロンモデルのことです。
を閾値とした場合のニューロンモデルのことです。
活性化関数にステップ関数![]() を用いて、パーセプロトンの出力
を用いて、パーセプロトンの出力![]() を表すと次のようになります。
を表すと次のようになります。
(2) 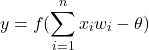
(3) 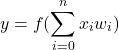
(3)式は![]() のときの入力
のときの入力![]() 、 重み
、 重み![]() と、閾値を和の形で表現しています。
と、閾値を和の形で表現しています。
単純パーセプトロンは、ニューラルネットワークの基本単位となる重要な物です。
重みと閾値を変化させることで、例えば「明日の天気予測」「顧客に最適な商品予測」などの様々なモデルを作成できます。
| – | 補足 |
|---|---|
| 実際のニューロンでは、入力信号の電位がある閾値を超えたときに、発火して信号を出力します。バイアス |
単純パーセプトロンの学習①勾配降下法
単純パーセプトロンでは、教師データを与えて勾配降下法(最急降下法)により、重みを決定します。
次のような誤差関数![]() が最小となるように繰り返し計算を行います。
が最小となるように繰り返し計算を行います。
| 数式 | 説明 |
|---|---|
| 誤差関数(損失関数) | |
| 重み | |
| 教師データ | |
| 教師データの 正解ラベル |
※正解ラベルtの値は、正解なら1, 誤りなら-1 |
重みの更新式
誤差関数![]() が大きいほど出力値に誤りが多いことを表します。
が大きいほど出力値に誤りが多いことを表します。
よって、これが最小になるように重み![]() を少しずつ動かして更新していきます。
を少しずつ動かして更新していきます。
更新の計算式は次のようになります。
(4) ![]()
| パラメータ | 説明 |
|---|---|
| 学習率: |
ずらす量(1より小さな値を設定。小さすぎると計算回数が増大) |
| 勾配値が正なら、負の方向に最小値があるので、そこへ動かすために |
注意
この誤差関数![]() を用いる場合、正解ラベルが
を用いる場合、正解ラベルが![]() なので活性化関数(ステップ関数)も次のように定義します。
なので活性化関数(ステップ関数)も次のように定義します。
(5) 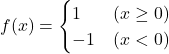
| – | 説明 |
|---|---|
| 1 | 初期パラメータ(学習率とエポック最大数)を設定します。 |
| 2 | 教師データ |
| 3 | 重み |
| 4 | 教師データ |
| 5 | 出力yと正解ラベルtを比較し、一致しなければ最急降下法で重みを更新します。 |
| 6 | 手順3~5をエポック最大数分だけ繰り返します。 |
Pythonによる実装例
関連記事

コメント