フーリエ変換の原理について入門者向けに紹介します。
フーリエ変換とは
フーリエ変換(Fourier Transform)とは、信号を時間領域から周波数領域に変換する処理です。
フーリエ変換では「一定の周期をもつ信号は複数の正弦波の和で表現できる」というフーリエ級数の性質を使って、周波数領域に変換します。
これにより、信号に「どのような周波数成分がどれだけ含まれているのか」を解析することができます。
変換後の信号、正弦波の和は![]() でなく、複素正弦波
でなく、複素正弦波![]() を使うため、複素数で表現されます。
を使うため、複素数で表現されます。
逆に、周波数領域に一度変換された信号を時間領域に戻すこともできます。
これを逆フーリエ変換(Inverse Fourier Transform)といいます。

【逆フーリエ変換】計算式の原理・意味
逆フーリエ変換(IFT)の公式と原理について入門者向けに紹介します。
フーリエ変換で周波数成分を解析する例
次のような周期的な入力信号![]() を用意します。
を用意します。
(1) ![]()
ここで周波数![]() [Hz], Noiseは雑音とします。
[Hz], Noiseは雑音とします。
![]() をフーリエ変換で周波数領域に変換すると
をフーリエ変換で周波数領域に変換すると![]() になります。
になります。
![]() から振幅スペクトル
から振幅スペクトル![]() を計算し、グラフ化すると以下のようになります。
を計算し、グラフ化すると以下のようになります。
■右が入力信号![]() 、左が振幅スペクトル
、左が振幅スペクトル![]()
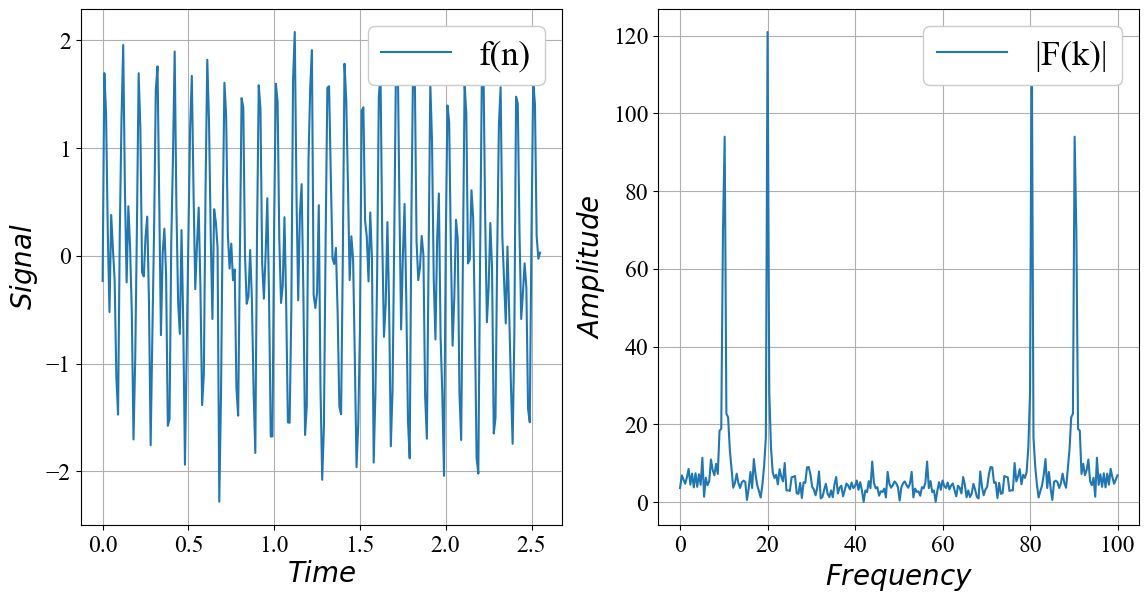
振幅スペクトル![]() を見ると、周波数
を見ると、周波数![]() のピークが大きいことがわかります。
のピークが大きいことがわかります。
これは、入力信号![]() に周波数
に周波数![]() の周波数成分が多く含まれていることを表しています。
の周波数成分が多く含まれていることを表しています。
このように、フーリエ変換で周波数領域に変換すると、入力信号の周波数成分を解析することができます。
フーリエ変換の計算式
任意の周期信号の時間領域を![]() 、(角)周波数領域を
、(角)周波数領域を![]() とします。
とします。
このとき、フーリエ変換の式は次のようになります。
(2) ![]()
![]() は各周波数、
は各周波数、![]() は時間、
は時間、![]() はネイピア数です。
はネイピア数です。
![]() は複素正弦波
は複素正弦波![]() の和となります。
の和となります。
ここで![]() ,
, ![]() ,
, ![]() をそれぞれ,
をそれぞれ,![]() の振幅スペクトル,位相スペクトル,パワースペクトルといいます。
の振幅スペクトル,位相スペクトル,パワースペクトルといいます。
関連ページ

【逆フーリエ変換】計算式の原理・意味
逆フーリエ変換(IFT)の公式と原理について入門者向けに紹介します。
【DFT】離散フーリエ変換の原理・計算式
この記事では、離散フーリエ変換(DFT)の公式と原理について入門者向けに紹介します。

高速フーリエ変換(FFT)の計算式の原理・意味
この記事では、高速フーリエ変換(FFT)の公式と原理について入門者向けに紹介します。

【高速フーリエ変換】ナイキスト周波数とサンプリング周波数の違いとエイリアシング
高速フーリエ変換(FFT)におけるナイキスト周波数とサンプリング周波数の違いとエイリアシングについてまとめました。


コメント