高速フーリエ変換(FFT)におけるナイキスト周波数とサンプリング周波数の違いとエイリアシングについてまとめました。
【数値例】高速フーリエ変換(FFT)
次のような周期信号![]() を用意します。
を用意します。
(1) ![]()
ここで![]() , Noiseは雑音とします。
, Noiseは雑音とします。
次に周期信号![]() をンプル数
をンプル数![]() 、サンプリング周波数
、サンプリング周波数![]() でデジタルの周期信号
でデジタルの周期信号![]() に変換します。
に変換します。
そして、デジタル周期信号![]() を離散フーリエ変換した結果は次の通りです。
を離散フーリエ変換した結果は次の通りです。
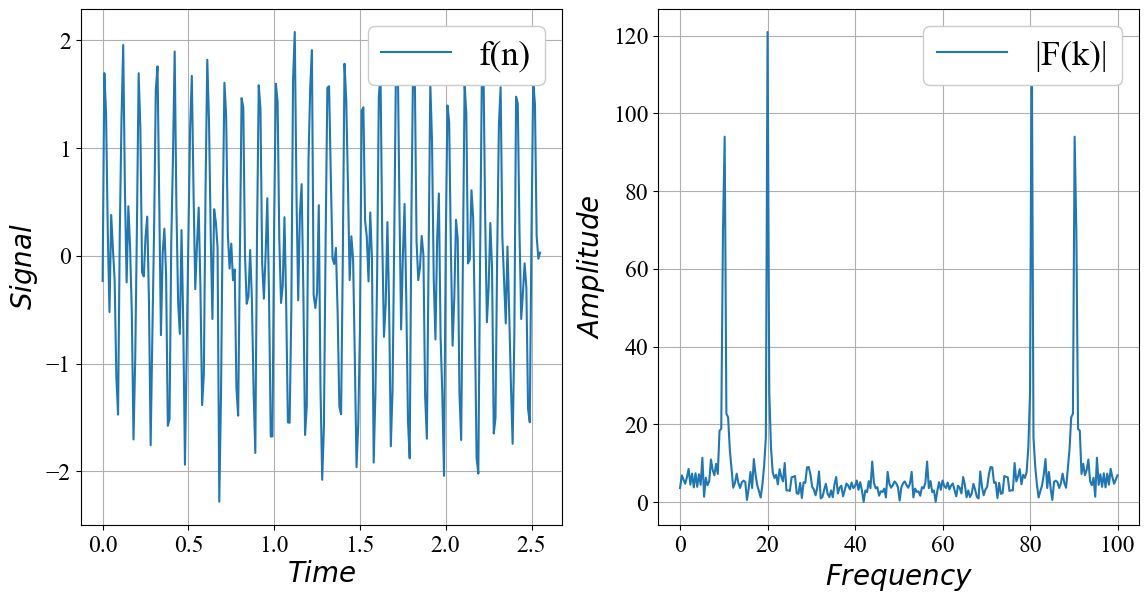
右が入力信号![]() 、左が振幅スペクトル
、左が振幅スペクトル![]() です。
です。
振幅スペクトルを見ると、周波数10, 20のピークが大きいことがわかります。
振幅スペクトルを見ると、低周波側(10, 20Hz)のスペクトルが大きいことがわかります。
これは、入力信号が2つの正弦波(周波数10と20)の合成波であるためです。
サンプリング間隔が0.01なのでサンプリング周波数は100Hzとなります。
高周波側(80, 90Hz)のスペクトルは、0Hz~50Hzの正の周波数(sin)に対して、-50Hz~0Hzの負の周波数(cos)に相当する成分です。
入力信号が実数の場合、低周波側と高周波側のスペクトルは対称になりますが、複素数の場合は非対称になります。
【エイリアシング】サンプリング周波数、ナイキスト周波数
| 用語 | 概要 |
|---|---|
| サンプリング周波数 |
1秒間にサンプリングされるデータ数です。例えば、サンプリング周波数 |
| ナイキスト周波数 |
サンプリングしたときに表現できる、周波数の最大値をナイキスト周波数 |
| エイリアシング | サンプリング周波数 |
関連ページ
【フーリエ変換】計算式の原理・意味
フーリエ変換の原理について入門者向けに紹介します。

高速フーリエ変換(FFT)の計算式の原理・意味
この記事では、高速フーリエ変換(FFT)の公式と原理について入門者向けに紹介します。
コメント