【逆フーリエ変換】計算式の原理・意味

信号処理

2017.10.292024.02.27

逆フーリエ変換（IFT）の公式と原理について入門者向けに紹介します。

目次

逆フーリエ変換
フーリエ変換の計算式
関連ページ

逆フーリエ変換

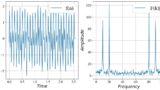
逆フーリエ変換（Inverse fourier Transform）とは、信号を周波数領域から時間領域に変換する処理です。
つまり、フーリエ変換の逆変換です。

フーリエ変換の計算式

任意の周期信号の時間領域を $f(t)$ 、（角）周波数領域を $F(w)$ とします。
このとき、逆フーリエ変換の式は次のようになります。

(1) $\begin{eqnarray*} f(t)=\frac{1}{2\pi}\int^{\infty}_{-\infty} F(w)e^{-jwt}dw \end{eqnarray*}$

$w$ は各周波数、 $t$ は時間、 $e$ はネイピア数です。

関連ページ

【フーリエ変換】計算式の原理・意味

フーリエ変換の原理について入門者向けに紹介します。

【逆フーリエ変換】計算式の原理・意味

逆フーリエ変換（IFT）の公式と原理について入門者向けに紹介します。

【DFT】離散フーリエ変換の原理・計算式

この記事では、離散フーリエ変換（DFT）の公式と原理について入門者向けに紹介します。

高速フーリエ変換（FFT）の計算式の原理・意味

この記事では、高速フーリエ変換（FFT）の公式と原理について入門者向けに紹介します。

【高速フーリエ変換】ナイキスト周波数とサンプリング周波数の違いとエイリアシング

高速フーリエ変換（FFT）におけるナイキスト周波数とサンプリング周波数の違いとエイリアシングについてまとめました。

コメント